Методы линейного построения массивов Suffix Array

Введение

Существует множество способов отсортировать массив с информацией (в частности текстовой информации). Одними из основных алгоритмов сортировки являются: сортировка вставками, сортировка Шелла и быстрая сортировка.

Сортировка вставками это один из простейших способов отсортировать массив. Как среднее, так и худшее время для этого алгоритма – O(n2).

Сортировка Шелла предложена Дональдом Л. Шеллом, и является неустойчивой сортировкой по месту. Эффективность метода Шелла объясняется тем, что сдвигаемые элементы быстро попадают на нужные места. Среднее время для сортировки Шелла равняется O(n1.25), для худшего случая оценкой является O(n1.5).

Хотя идея Шелла значительно улучшает сортировку вставками, резервы еще остаются. Один из наиболее известных алгоритмов сортировки – быстрая сортировка, предложенная Ч. Хоором. Этому методу требуется O(n lg n) в среднем и O(n2) в худшем случае. К счастью, если принять адекватные предосторожности, наихудший случай крайне маловероятен. Быстрый поиск не является устойчивым. Кроме того, ему требуется стек, т.е. он не является и методом сортировки на месте.

Оценки времени исполнения

Для оценки производительности алгоритмов можно использовать разные подходы. Один из способов – оценить время исполнения. Например, мы можем утверждать, что время поиска есть O(n) (читается так: о большое от n). Это означает, что при больших n время поиска не сильно больше, чем количество элементов. Когда используют обозначение O(), имеют в виду не точное время исполнения, а только его предел сверху, причем с точностью до постоянного множителя. Когда говорят, например, что алгоритму требуется время порядка O(n2), имеют в виду, что время исполнения задачи растет не быстрее, чем квадрат количества элементов. Чтобы почувствовать, что это такое, посмотрите таблицу 1.1, где приведены числа, иллюстрирующие скорость роста для нескольких разных функций. Скорость роста O(lg n) характеризует алгоритмы типа двоичного поиска. Логарифм по основанию 2, lg, увеличивается на 1, когда n удваивается. Вспомните – каждое новое сравнение позволяет нам искать в вдвое большем списке. Именно поэтому говорят, что время работы при двоичном поиске растет как lg n.

Таблица: Скорость роста нескольких функций

Итак, как видно из таблицы, самым оптимальным решением является сортировка, которая выполняется в линейное время. Для этого Manber и Myers была разработана структура данных  названная массивом суффиксов.

Называем суффиксом любую часть строки от i-той позиции до конца строки n. Например, все суффиксы которые можно получить из строки MISSSISSIPPI:

Массив суффиксов SArray (T) строки T - это лексикографически отсортированный массив суффиксов (T), где каждый суффикс представлен его стартовой позицией. Пример показан в рисунке.

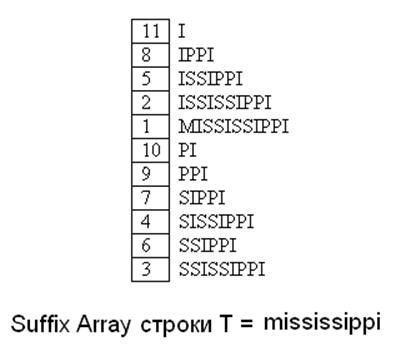
Особенность этой структуры данных является то, что разработаны алгоритмы позволяющие получать Suffix Array за линейное время.

Массив суффиксов имеет многочисленные приложения в поиске образца, в заданной строке (например, при поиске какой либо строчки в исходном тексте, или при поиске информации в глобальной сети) а так же вычислительной биологии и других приложениях.

Существует несколько алгоритмов построения массивов SA  самый простой из них это последовательного перебора всех суффиксов, но в тоже время скорость его выполнения отставляет желать лучшего.

Алгоритм построения SAпоследовательным перебором всех суффиксов.

1.  Каждый суффикс строки нумеруется последовательно  слева направо начиная с цифры 1 

2.  Потом выписываются все суффиксы в не отсортированном порядке.

3.  Следующим этапом выбирается минимальный суффикс и его номер заносится в первую позицию SA

4.  Далее берется следующий минимальный суффикс и его номер переносится на вторую позицию массива SA и так далее пока не закончатся все суффиксы.

5.  В итоге получаем упорядоченный в возрастающем порядке массив суффиксов исходной строки.   

Последние три этапа можно заменить любым алгоритмом сортировки, который бы упорядочил массив по возрастанию. Но, к сожалению, все обычные алгоритмы сортировок, примененные к массиву суффиксов выполняются непозволительно долго. В связи, с чем были разработаны алгоритмы, которые выполняются в линейное время. Одним из таких алгоритмов является алгоритм разработанный Julia Karkkainen, Peter Sanders

Алгоритм построения SA в линейное время предложенный Sanders

Этот алгоритм намного более прост, чем предыдущие линейные алгоритмы времени, которые базируются на более сложной структуре данных  - дерева суффиксов. Так как сортировка - хорошо изученная проблема, мы получаем оптимальные алгоритмы для нескольких других моделей вычисления, например внешняя память с параллельными дисками, кэш, забывающий, и параллельный.

Введем искажающийся алгоритм для построения массива суффиксов состоящего из алфавита целых чисел, который может быть выполнен, в линейное время, используя сортировку целых чисел, как единственную нетривиальную подзадачу: