Расчет генератора на ТТЛ-элементах (155 серия) со сложным инвертором и открытым коллектором, страница 2

Подставляя данное значение в (5), можем получить зависимость времени от емкости на участке t₁-t₂ (рисунок 12):

Определим, зависимость времени зарядки конденсатора от емкости на первом участке. Для этого решим дифференциальное уравнение (2):

Определим константу C1 исходя из того, что конденсатор в начальный момент времени будет заряжен до напряжения 0,8 В, и подставим ее в полученное решение:

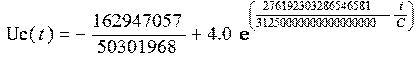
Теперь, считая, что конденсатор будет перезаряжаться до напряжения -1,1 В определим зависимость времени от емкости на участке t₀-t₁ (рисунок 12):

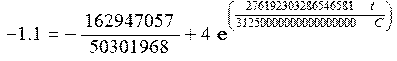
Таким образом, получаем, что по расчетам скважность импульсов почти равна двум и период следования сигналов равен 144С.

Проверим сделанные выводы на практике. Ниже приведены реально снятые осциллограммы сигналов. При снятии осциллограмм использовалась микросхема К155ЛН1 и конденсатор емкостью 0,05 мкФ. Для улучшения формы сигнала добавлялся еще один инвертор.

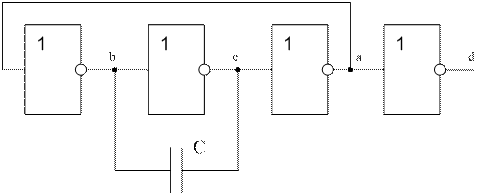
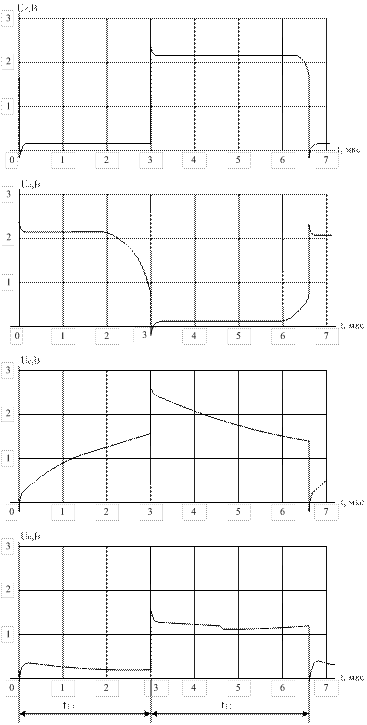
Рисунок 12.  Снятые осциллограммы сигналов (С = 0,05мкФ)

Анализируя практически снятые характеристики, при учете того, что осциллограф исправный и работает в пределах погрешности, можно отметить следующее:

- период следования импульсов равен ;

- скважность сигнала равна 1,8;

-

Таким образом, получаем, что емкость сверху будет ограничена допустимой длительностью фронта критического режима (протекает ток короткого замыкания) для данных элементов, а снизу ограничена быстродействием элементов и требуемой крутизной фронта.

Рассчитаем и проанализируем работу генератора построенного на основе элементов ТТЛ (155 - серия) с открытым коллектором. Если предыдущая схема работала в критическом режиме, так как при переключениях в цепях заряда/разряда конденсатора протекали значительные токи, то в данном случае мы можем самостоятельно ограничить выходные токи по единице.

Будем считать, что для элементов с открытым коллектором изменятся лишь выходные характеристики по единице. Примем также то, что для работы схемы в нормальном режиме выходные токи по нулю не должны превышать 10 мА. Тогда для ЛЭ1 коллекторный резистор будет равен: 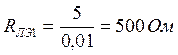. Принимая то, что ток не ответвляется во входные цепи ЛЭ2 и ЛЭ3. Для элемента ЛЭ2 коллекторный резистор составит величину:

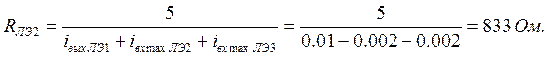 Для ЛЭ3 все проще ему достаточно обеспечить мизерный входной ток ЛЭ1 (40-50 мкА), поэтому примем его равным 10 кОм. Теперь построим выходные характеристики для ЛЭ1 и ЛЭ2:

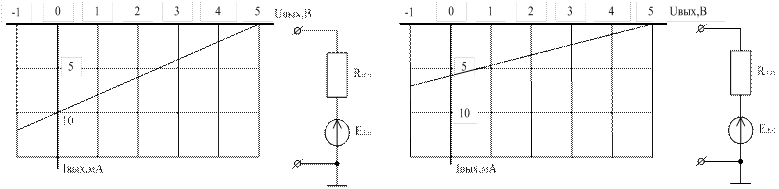
Рисунок 13. Выходные характеристики ЛЭ1 и ЛЭ2 и их эквивалентные схемы

Номиналы эквивалентных схем следующие: Е_ЛЭ1=Е_ЛЭ2=5 В, R_ЛЭ1=500 Ом, R_ЛЭ2=800 Ом.

Эквивалентная схема первого отрезка времени соответствует схеме представленной на рисунке 10, а описывается соответственно системой 1. Подставив соответствующие значения сопротивлений и ЭДС, получим:

                (6)

Определим, до какого значения зарядится конденсатор до переключения ЛЭ3. ЛЭ3 переключится в момент когда напряжение в точке b достигнет уровня 1,3 В. Оценим ток протекающий в этот момент в  выходной цепи ЛЭ2 и определим исходя из этого заряд на конденсаторе. Падение напряжения на R3 должно составлять E3-Ub=5B-1,3B=3,7 В для того чтобы в точке b потенциал составил 1,3 В. Следовательно ток через резистор R3 составит 4,6 мА. Ток в выходной цепи складывается из тока текущего через С и входного тока ЛЭ3, его аналитическое выражение:

, откуда Uc= -1,2 В.

Теперь рассмотрим схему во второй момент времени когда ЛЭ1 находится в состоянии единицы по выходу а ЛЭ2 и ЛЭ3 в состоянии нуля. Эквивалентная схема для этого момента времени представлена на рисунке 11 и описывается системой уравнений (3). Решая эту систему, получаем:

                                       (7)

Решим полученное дифференциальное уравнение (7):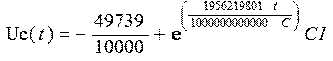

Определим константу С1, исходя из того, что в момент времени t₁ напряжение на конденсаторе равно -1,2 В:

Таким образом, уравнение принимает вид:

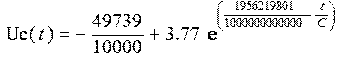                                                  (8)

Посчитаем, какое напряжение будет на конденсаторе при достижении в точке b уровня напряжения 1,3 В. Для этого составим следующее уравнение: . Решая данное уравнение получаем Uc=0,7 В.

Подставляя данное значение в (8), получаем зависимость времени от емкости на участке t₁-t₂:

Определим, зависимость времени зарядки конденсатора от емкости на первом участке. Для этого решим дифференциальное уравнение (6):

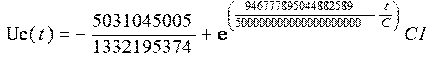
Определим константу C1 исходя из того, что конденсатор в начальный момент времени будет заряжен до напряжения 0,7 В, и подставим ее в полученное решение:

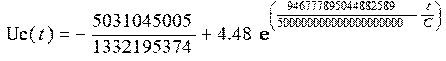
Теперь, считая, что конденсатор будет перезаряжаться до напряжения   -1,2 В определим зависимость времени от емкости на участке t₀-t₁:

Таким образом, получаем, что период следования сигналов равен ~500С.

Ниже приведены реально снятые осциллограммы сигналов. При снятии осциллограмм использовалась микросхема К155ЛН5 и конденсатор емкостью 0,05 мкФ.

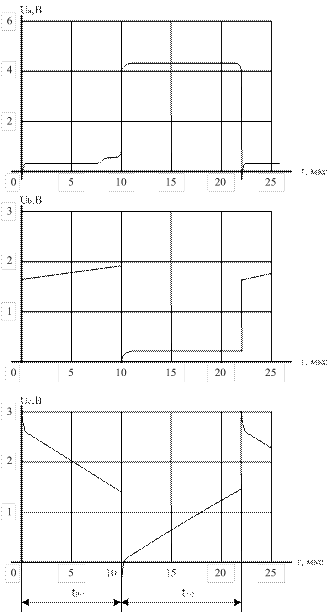
Рисунок 14.  Снятые осциллограммы сигналов генератора на элементах с открытым коллектором (С = 0,05мкФ)

Анализируя полученные результаты, можно отметить, что для элементов с открытым коллектором значение ёмкости снизу также ограничено быстродействием элементов и требуемой крутизной фронта, а сверху не ограничена, т.е. если мы замкнём ёмкость накоротко, то элементы просто не будут переключаться, но не сгорят. Естественно, что приведенные нами расчёты не приемлемы в крайних ситуациях.

Вывод: В результате проделанной работы рассчитали генератор на элементах ТТЛ со сложным инвертором и открытым коллектором. Несоответствие реально снятых осциллограмм от теоретически выведенных формул можно объяснить следующим. Во-первых, использовались характеристики для элементов Texas Instruments, к тому же аппроксимация характеристик приводит к неточности расчётов. Во-вторых, использовались статические характеристики элементов, а рассчитывалась динамика, что значительно сказывается на точности расчетов для высоких частот работы генератора. В-третьих, влияет погрешность измерительной аппаратуры (осциллографа). И, в-четвертых, неточность параметров применяемых элементов.