Микропроцессорная система коррекции режимов работы двигателя внутреннего сгорания (Проектная часть дипломного проекта)

2.  Проектная часть

2.1. Упрощенная математическая модель рабочего процесса ДВС

Для анализа свойств двигателя, как объекта регулирования необходимо построение математической модели его работы в виде дифференциальных уравнений.

Дифференциальные уравнения позволяют связать статические характеристики работы двигателя со временем, т.е. проанализировать неустановившиеся режимы работы. Таким образом, все (или некоторые) параметры работы двигателя, входящие в функциональную зависимость (1.5), при неустановившихся условиях работы с течением времени получают алгебраические приращения и в связи с этим становятся зависимыми от времени. Поэтому вся совокупность значений параметров зависимости (1.5) имеет смысл лишь для конкретно выбранного момента времени.

Рассмотрим упрощенную модель части рабочего процесса.

Для оценки двигателя как регулируемого объекта первостепенное значение имеют статические характеристики двигателя в целом и отдельных его элементов (Рис. 2.1-2.3).

В двигателе в зависимости от изменения угла опережения зажигания происходит изменение крутящего момента и скорости вращения коленчатого вала. На валу ДВС имеется момент сопротивления от нагрузки. Разность крутящего момента и момента сопротивления расходуется только на ускорение (замедление) выходного вала двигателя. Приведенный к валу двигателя  суммарный момент инерции всех масс можно считать постоянным. В этом случае уравнение вращающихся масс двигателя можно записать в виде   

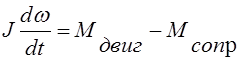,                   (2.1)

где J - момент  инерции всех вращающихся масс, приведенных к выходному валу двигателя, w - циклическая частота вращения вала двигателя (w=2pn),  M_двиг - движущий момент на валу, M_сопр - момент сопротивления на валу двигателя.

;                         

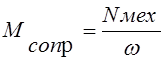Исходя из этих  равенств:

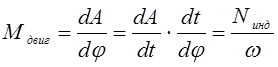,             (2.2)

Подставляем полученные выражения в формулу (2.1) и получаем

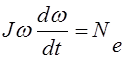.                                      (2.3)

Обобщенные характеристики [2] для N_e приведены на Рис. 2.1-2.3.

Из приведенных характеристик видно, что они не имеют разрывов и плавно изменяются, поэтому допустима их линеаризация. Рассматривая малые отклонения переменных от принятых установившихся значений, запишем

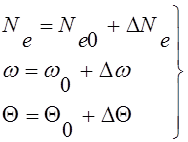         (2.4)

Разложим в ряд Тейлора правую часть (2.3)

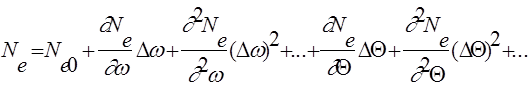            (2.5)

Для линеаризации нелинейного уравнения  N_e=N_e(w,Q) воспользуемся лишь линейными членами в уравнении (2.5); тогда

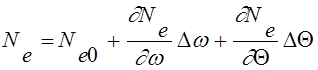,                          (2.6)

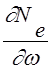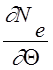где  - тангенс угла наклона касательной к кривой N_e, построенной в зависимости от w;  - тангенс угла наклона касательной к кривой N_e, построенной в зависимости от Q, в точке установившегося режима работы (точка О).

В процессе регулирования характеристика N_e меняется не на всем протяжении изменения w и Q, а лишь в определенных пределах. Тогда можно считать, что в зависимости от времени угловая скорость вала двигателя изменяется относительно установившегося значения w₀ на малую величину Dw, и реальные нелинейные характеристики в определенных пределах изменения переменных можно заменить линейными. Такая замена нелинейной характеристики называется линеаризацией характеристики.

Подставляя выражение (2.4) в уравнение (2.1), получаем

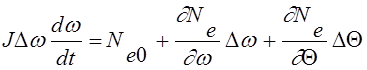.                                      (2.7)

Выражение (2.5) представляет собой упрощенное линеаризованное уравнение работы двигателя в приращениях. Уравнение упрощенное, т.к. в нем не учитываются такие факторы как процент открытия дроссельной заслонки, среднеэффективное давление, удельный расход топлива и т.д.

Введем в уравнение (2.5) следующие обозначения:

;      ;     ;  ; ;

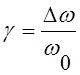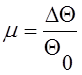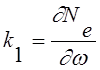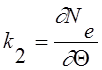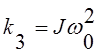После преобразований получим окончательную форму уравнения

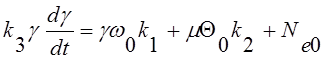.                                   (2.8)

Полученное выражение показывает, что изменение эффективной мощности двигателя связано с изменением, в первую очередь, угла опережения зажигания в зависимости от частоты вращения коленчатого вала двигателя.

Анализ параметров, влияющих на эффективную мощность двигателя согласно формуле (1.5), показывает, что число этих параметров,  удельный вес каждого из них определяется типом двигателя и требованиями потребителя. Например [13], изменение эффективной мощности зависит от изменений цикловой подачи топлива и эффективного КПД, причем влияние эффективного КПД тем больше, чем больше проявляется нехватка воздуха для полного сгорания топлива.

2.2. Построение адаптивной системы и системы на основе данных коррекции ПЗУ

Для получения оптимальных характеристик (либо по экономичности, либо по мощности двигателя) основной задачей системы автоматического регулирования параметров ДВС  является управление, во-первых,  подачей топлива, во-вторых моментом зажигания. При изменении частоты вращения коленчатого вала двигателя, как известно, требуется изменение длительности впрыска топлива, и соответственно изменение момента зажигания. При этом, при правильном выборе коррекции этих сигналов, текущая индикаторная характеристика двигателя будет близка к оптимальной, при превышении которой следует детонационный процесс горения (и как следствие потеря мощности).