Полнота логических функций. Теорема дедукции. Свойства формальных теорий (логических систем). Равносильные формулы логики предикатов, страница 8

Замечание 1.  (внешний алфавит)

Символы МТ состоит из двух символов А.

Замечание 2.   

Опр.

Стандартной начальной конфигурацией называется :

 

- начальное состояние Машины.

Опр.

Стандартной заключительной (конечной) ситуацией называется :

Опр.

Арифметическая функция называется правильно вычисляемая на МТ, если

1) Функция определена     , то существует конечное состояние.

                        2) Функция не определена   не определена

Пр.

, если , то, если  то ,   

(начальная конфигурация)  (конечная конфигурация)

1)   

		1	1	1	1

- ничего не будет делать, а переместиться вправо (R).

2)                        

		1	1	1	1

3)                        

		1	1	1	1

4)                           

		1	1	1	1	0

5)                            

		1	1	1	1	0

6)                          

	0	1	1	1	1	0

7)                                               

0	0	1	1	1	1	0	0

1-й способ задания- список.

2-й способ задания – таблица :

	1	0

3-й способ задания – граф :

                                                                

.                                        

.                               

§2. Примитивно – рекурсивные функции

Опр.

            0() – называется такая функция, которая на любом числе = 0,  

Опр.

Функция следования

Замечание.

С помощью 0() и s() можно получить весь числовой ряд (N).

Опр.

Функцией проекции называется :

Которая по n – переменных перехватывай только i-ю переменную. ()

Опр.

0(), s(),- называются элементарными, если они образуют базис (иногда называются базисные)

Опр.

Оператором суперпозиции называется такое отображение :

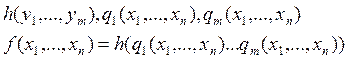
Замечание.

Если переменные меньше n , то считать недостаточно фиктивные.

Пр.

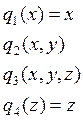
Опр.

Оператором примитивной рекурсии называется такое отображение, которое по функциям  и получает .       .

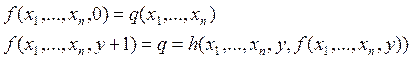
Принцип математической индукции (схема примитивной рекурсии)

Опр.

Примитивно рекурсивной функцией называется :

1)Все элементарные функции.

2) Все функции полученные из элементарных с помощью операторов суперпозиции

 и оператора примитивной рекурсии , за конечное число шагов.

Пр.

1) - ПРФ

Решение :

                

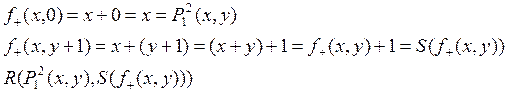
Опр.

Оператор минимизации  

                                                                                                                     

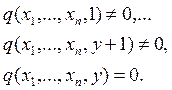
Наименьшее y при котором g(…) зануляется.

Опр.

Функция называется частично рекурсивной, если:

1)  Она ПРФ.

2)  Получена из ПРФ с помощью оператора минимизации.

Опр.

Если ЧРФ всюду определена, то она называется общерекурсивной функцией.

Замечание.

Опр.

Вычислимой называется такая функция для которой существует вычисляющий её алгоритм.

Тезис Чёрча.

Класс вычислимых функций совпадает с классом ЧРФ, т.е. всякая вычислимая функция является ЧРФ и наоборот.