Математика \ Математическая логика и теория алгоритмов

Полнота логических функций. Теорема дедукции. Свойства формальных теорий (логических систем). Равносильные формулы логики предикатов, страница 5

выполняется = 0, во всех остальных случаях.

, где {0,1}– одноместный предикат.

Замечание 1 :

выполняется

Опр. 1, если , при некотором ,

выполняется = 0, в противном случае.

Здесь {0,1} – одноместный предикат.

Замечание 2 :

выполняется = - тождественно истинный на

Замечание 3 :

Пусть {0,1}

Если множеством предиката является конечное множество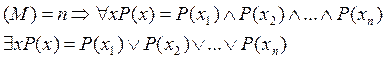

Замечание 4 :

и - переменная - связанная.

От неё ничего не зависит, она является символом.

Пр.

- двуместный предикат, а при - одноместный предикат.

- связанная переменная, т.к. стоит под квантором всеобщности.

- свободная переменная.

Замечание 5 :

Операции квантования не коммутативны.

Пр.

: “для каждого выполняется ”

: ”для каждого и для каждого выполняется ” =0.

: “для любого найдётся : ” =1.

: “есть такой , что при любом : ” =0.

§ 3. Равносильные формулы Логики предикатов

Опр.

Формулой логики предикатов называется :

1) Все элементарные высказывания из алгебры высказываний.

2) , где - предметные переменные- область определения предиката.

- определённый предикат.

3) Если и - формулы Л.П. ( причём, если некоторая предметная переменная , то она не может быть и связанной и свободной), то & тоже формулы Логики предикатов.

4) и - формулы, где - формула Л.П., - предметная переменная.

5) Других формул Л.П. нет !

Опр.

Два предиката называются равносильными на множестве , если они принимают одинаковые значения на .

Опр.

Два предиката называются равносильными, если они равны на любом множестве своейобласти определения.

Пр.

” - чётное”,

” делится нацело на 2”,

, на любом множестве.

” делится нацело на 6”,

и равносильны не на любом множестве, а на ={6,12,24,3}

6,12,24},

6,12,24}, = на .

Если {6,12,24,3} , то

6,12,24}, то на

Замечание.

Т.к. все формулы Алгебры высказывания 1)-3), то и все законы Алгебры высказывания переносятся в Логику предикатов.

I I)

I I I)

IV)

V) &&

VI)

VII) &&

VIII)

I Х)

Х) &&

Х I)

Х I I)

Х I I I)

Х IV)

§ 4. Нормальные формы Л.П.

Опр.

Формула Л.П. называется нормальной, если она содержит &, а стоит над формальной переменной и .

Замечание 1.

Любая формула Логики предикатов приводит к нормальному виду.

Т.к. и можно расписать.

Опр.

Предварённая Н.Ф. называется Н.Ф. следующего вида :

где - кванторы .

- формула Л.П. с предметными переменными не содержат кванторов.

Теорема.

Любую формулу Логики предикатов можно привести а предварённой Н.Ф.

Пр.

&&&&&

Исчисления предикатов

§ 1. Понятие И.П.

Опр.

Исчислением предикатов называется следующая система : <> :

1) - алфавит.

1.1) … - пропозициональные переменные.

1.2) … - предметные переменные.

1.3) … предикатные переменные.

- целые (местность предиката, например : -местный предикат.)

1.4) &, - логические связки.

1.5) - кванторные связки.

1.6) “ ( “ , “ ) ” , “ , ”

2) Ф - множество букв (множество формул И.П. , т.е. слов)

2.1) Все пропозициональные переменные формулы И.П.

2.2) - формулы И.П., где - предметные переменные (свободные)

- предикатная переменная.

2.3)Если а() – формула И.П., где - свободная переменная а(), а() – формулы И.П., где - свободная переменная.

2.4) Если определены некоторые формулы а, в – формулы И.П.а , а&в , ав , ав , формулы И.П., причём не существует переменной : в а – связанных , а в в – свободных.