Построение эпюр поперечных сил, изгибающих моментов и выбор сечений балок. Вариант № 4, страница 3

Dl₁ = ВВ’= О₁В – l₁ = 0

Dl₂ = C”C’ = O₂C’ – l₂ .

Из геометрии: ÐО₂CC” = ÐC”CC’ = a₂

Определение усилий от внешней силы Р.

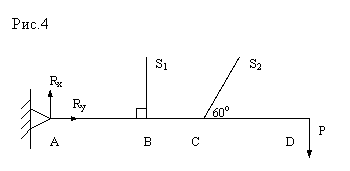
Для расчета усилий используем метод РОЗУ. Сечения проводим через оба стержня. Рассмотрим равновесие нижней части системы, заменяя действие отбрасываемой верхней части стержней внутренними усилиями реакций S₁ и S₂.

 

Рассматриваемая система является плоской системой произвольно расположенных сил. Для нее справедливы три закона равновесия. Два из них касаются реакций R_x и R_y в шарнире. Так как условием задачи нахождение этих реакций не требуется, то составим одно необходимое уравнение статики:

SМ_А = S₁a×sina₁ + S₂(a+b)sina₂ – P(a+b+c) = 0

так как a₁ = 90^о, то sin 90^о = 1  Þ 

S₁a+S₂(a+b)sina₂ = P(a+b+c)

Таким образом, число уравнений статики – 1, а число неизвестных усилий – 2. Следовательно, степень статической неопределимости системы: А = N – K = 1.

Для составления уравнения совместности деформаций можно воспользоваться подобием треугольников АВВ’ и АСС’:

Из DBB’B” и DCC’C” получим:

 ;                              

Подставив равенства (2) в формулу (1),получим уравнение совместности деформаций заданной стержневой системы:

или  Dl₁ = Dl₂ k  , где     – безразмерный коэффициент, учитывающий особенности геометрической конфигурации системы. Используя закон Гука для каждого из стержней:

;                          

Из уравнения (2) получим:

Учитывая, что l₁ = h×sin90^o=h;  l₂= h×sin60^o, соотношение можно переписать так:

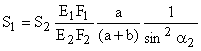
Решая совместно систему уравнений (2) и (6), получим:

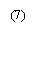
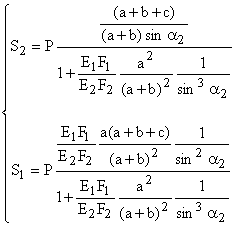
Значения всех использованных величин известны, находим численные значения усилий:

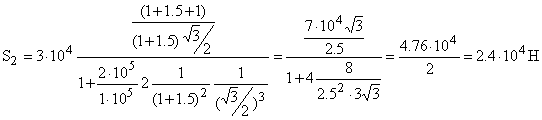
Стержень 2 испытывает растяжение.

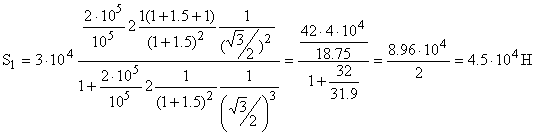
Стержень 1  также испытывает растяжение.

Проверка правильности найденных числовых значений производится путем подстановки значений в уравнение равновесия (2):