Лабораторная работа №1.Общая постановка задач дискретизации.
1.1а Импульсным откликом называется обратное преобразование Фурье передаточной функции:
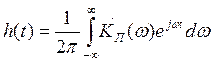
Определить импульсный отклик идеального датчика, описываемого соотношением:
![]() (передаточная
функция по амплитуде);
(передаточная
функция по амплитуде);
![]() (передаточная
функция по фазам).
(передаточная
функция по фазам).
Решение: Передаточная функция по амплитуде определяется как:
![]() ,
,
Þ 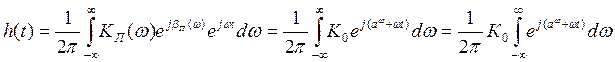 .
.
1.1б Сигнал u(t) квантуется по времени с шагом Тв. Ширина квантованных импульсов постоянна и равна t. Построить (качественно) графики спектральных функций квантованного сообщения при различных соотношениях между Тв и t.
Решение:Спектральная функция квантованного сообщения:
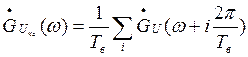 , где
, где
![]() - это спектральная
функция сообщения u(t).
- это спектральная
функция сообщения u(t).
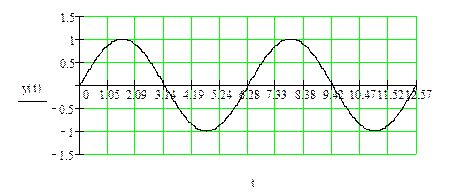 Непрерывная функция y(t)=sin(t):
Непрерывная функция y(t)=sin(t):
Спектральная функция квантованного сообщения при Тв>t:
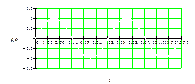 |
Спектральная функция квантованного сообщения при Тв=t:
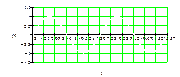 |
Спектральная функция квантованного сообщения при Тв<t:
 |
1.1в Непрерывное сообщение квантуется по уровню и по времени на основе частотного (теоремы Котельникова) и квантованного критериев. В каких пределах изменяется интервал квантования Тв, если производная функции меняется в пределах от 0 до 10 условных единиц в секунду, граничная частота равна 50Гц. и шаг квантования по уровню равен 0,08 условной единицы?
Решение:
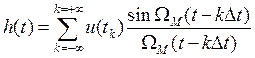 , где
, где 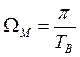 - высшая частота спектральной функции,
- высшая частота спектральной функции,
![]() - интервал корреляции.
- интервал корреляции.
Шаг квантования: 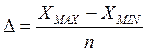 , Þ
, Þ
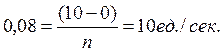 ,
,
Þ число уровней квантования: n = 125.
Т. к. ![]() , Þ
, Þ 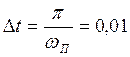
![]() ,
, ![]()
Þ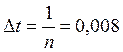
Отсюда получим, что интервал квантования может изменяться от 0,008 до 0,01.
1.1г При оптимальном квантовании по уровню, учитывающем статистические характеристики непрерывного сигнала, более вероятные значения квантуются, с меньшим шагом, а менее вероятные - с большим. Известно, что дисперсия шума квантования выражается при этом следующим образом:
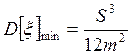 , где
, где 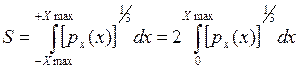
- функция, зависящая от распределения ![]() непрерывного сигнала Х(t),
m - число уровней квантования. Определить дисперсию
шума квантования в случае нормального распределения входного сигнала Х(t) с функцией плотности
непрерывного сигнала Х(t),
m - число уровней квантования. Определить дисперсию
шума квантования в случае нормального распределения входного сигнала Х(t) с функцией плотности
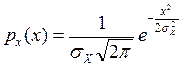 .
.
Решение:
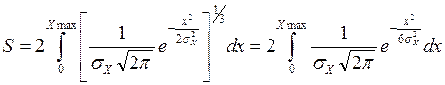 ,
,
Þ 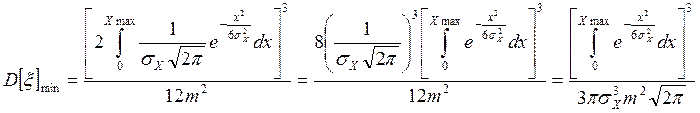 .
.
Лабораторная работа №2.Количественная оценка информации.
2.1а Вычислить автокорреляционную функцию стационарного случайного процесса: Х(t)=Acos(wt+Q), где Q - случайная величина.
Решение:Для эргодического
процесса корреляционная функция: 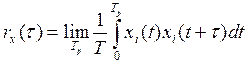 ,
,
Þ
2.1б Имеются два дискретных источника информации, заданные матрицами:
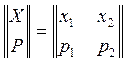 ;
;
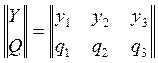
Определить, какой источник обладает большей неопределенностью в случае, если: а) p1= p2, q1= q2= q3; б) p1= q1, p2= q2+ q3.
Решение:
а) 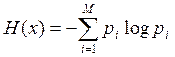
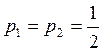 , Þ
, Þ
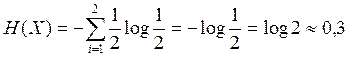
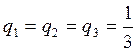 , Þ
, Þ
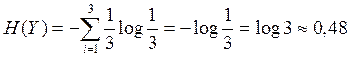
Þ H(Y)>H(X)
б)![]()
![]()
Т. к. log(q2+q3)³logq2 & log(q2+q3)³logq3
Þ H(Y) ³H(X)
2.1в Имеются два дискретных источника с независимыми и равновероятными элементами: двоичный и троичный. На выходе первого источника зафиксированы два символа, на выходе второго - три. Чему равны неопределенности полученных последовательностей букв, образованных парами символов первого источника и тройками символов второго?
Решение:
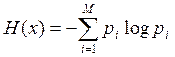
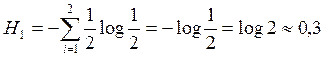
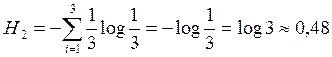
2.1г Записать соотношения между энтропиями: H(x), H(y), H(x|y), H(y|x), H(x,y), H(x|yi), H(y|xi).
Решение:
Если x и y независимые, тогда:
H(x) » H(y);
H(x|y)< H(x|yi) < H(x);
H(y|x) < H(y|xi) < H(y).
Если x и y зависимые, тогда:
H(x|y) < H(x);
H(x|yi) = H(x);
H(y|xi) = H(y);
H(y|x) < H(y).
H(x,y) ≤ (H(x)+ H(y))
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.