Детальный проект конвейерного RISC процессора (Глава 5 "Обработка прерываний"), страница 6

Последовательность команд SAVE H RESTORE называется образцом ISR(j) если в течении H уровень прерывания равен

il = j.

Она называется не прерывающимся выполнением ISR(j) если уровень прерывания подчиняется

il   =   jв течении save и restore

il   <=   jв течение H.

Таким образом, в течение выполнения ISR(j) обработчик H(j) может быть прерван. Мы не рассматриваем бесконечное выполнение.

Предположим, что H не заканчивается последовательностью restore уровня  прерывания j, тогда

save₁ h SAVE₂ H' restore

называется прерывающимся выполнением ISR(j) если

il  =    jв течении SAVE₁

il  <=  jв течении H

il  <=  2   в течении SAVE₂, H' и RESTORE.

Мы называем выполняющуюся процедуру обработки прерываний правильно вложенной или проще вложенной, если

1. прерван не кодовый сегмент save или restore,

2. последовательность кодовых сегментов save и restore формирует начальный сегмент соответствующей скобочной структуры, и если

3. парные скобки принадлежат примеру некоторого ISR(j) в следующем значении: Пусть Lи Rпарные последовательности save и restore. Пусть H состоит из команд между Lи R

(a) которые не принадлежат последовательностям save и restore, и

(b) которые не включаются парными скобками внутрь Lи R.

Тогда LHRобразец некоторого ISR(j).

Мы называем выполнения совершенно вложенными (perfectlynested) если они правильно вложены и последовательность saves и restores формирует соответствующую скобочную структуру. В следующих доказательствах мы установим, что

Выполняющиеся допустимые процедуры обработки прерываний являются  правильно вложенными,

Сперва мы установим свойства вполне вложенных выполнений процедур обработки прерываний в лемме 5.3.  В лемме 5.4 мы докажем

индукцией существование скобочной структуры. В шаге индукции мы применим лемму 5.3 к части скобочной структуры, чье существование уже гарантировано индукционной гипотезой.  В частности, нам нужны некоторые усилия для доказательства, что restores никогда не прерывается. Тогда теорема следует непосредственно из лемм 5.3 и 5.4.

Пусть механизм прерывания подчиняется программным ограничениям 1 - 3. Рассмотрим совершенное вложенное выполнение ISR(j). Последовательность выполняемых команд имеет форму

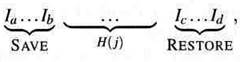
тогда мы имеем:

1. Если выполнение ISR(j) не прервано, тогда стек прерываний IS хранит одно и то же количество кадров до и после ISR(j), и сегменты IS, зарезервированные для регистров HER, остаются неизменными, т.е.,

ISP_a-1 = ISP_d    и   IS.EHR_a-1 = IS.EHR_d .

2. Точность. Если ISR(j) не прервано, выполнение продолжается с

Доказательство индукцией по числу nпрерываний, которые прерывают выполнение ISR(j).

n = 0. Выполнение ISR(j) непрерывно. Так как прерывание j является непрерывным, save размещает новый кадр на стеке IS а restore снимает один кадр. Обработчик H(j) сам не изменяет указатель стека (ограничение 1), таким образом

ISP_a-1 = ISP_d .

Согласно ограничению 1, поля EHR на стеке прерываний ISпишутся только SAVE. Однако SAVE просто модифицирует один кадр IS, который удаляется restore. Таким образом

IS.EHR_a-1 = IS.EHR_d ,

и требование 1 выполняется. Что касается требования 2, мы покажем только точность масок SR; точность PC может быть показана тем же путем.

SR_d   =   ESR_d-1                                      по определению rfe

=   IS.TOP.ESR_c-1по определению restore ,

где IS.TOPозначает верхний кадр стека IS. Так как сам обработчик не модифицирует ни указатель стека ISP, ни поля EHR на стеке IS (ограничение 1), из этого следует

IS.TOP.ESR_c-1    =   IS.TOP.ESR_b

=   ESR_a-1                               по определению save ,

и по определению влияния JISRтогда следует, что

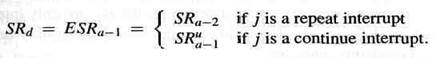
В шаге индукции мы решаем от n до n+ 1. Выполнение ISR(j) прерывается n+1 прерываниями, и коды SAVE и RESTORE соответствующих примеров ISR формируют надлежащую скобочную структуру. Так как save и restore непрерывны, существует mверхнеуровневых пар скобок в потоке команд обработчика H(j); каждая пара соответствует примеру ISR( j_r ):

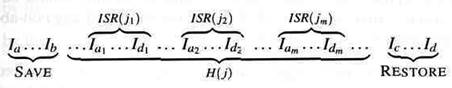
Каждый ISR( j_r ) прерывается самое большее nраз, и из-за индукционной гипотезы они возвращают указатель ISPи поля EHR на стек неизмененными:

Так как команды обработчика H(j) не изменяют эти данные, из этого следует для указателя ISP, что