Оценка точности прямых и косвенных измерений физических величин, страница 2

Измеряя диаметр прибором более точным, например микрометром, получим серию результатов: , где n - число измерений. Как величина случайная диаметр варьирует около некоторого среднего значения, которое определяется как среднее арифметическое:

.

Величина средней абсолютной ошибки

.                                       (3)

В случае, если она меньше точности используемого прибора, то за величину абсолютной ошибки следует принять последнюю.

Измерения величины тока I и напряжения U проводят с помощью электроизмерительных приборов (амперметра и вольтметра).  Точность этих приборов характеризуют приведенной погрешностью

где х_пр - наибольшее значение величины, которое может быть измерено по шкале прибора.

Приведенная погрешность, измеренная в процентах, определяет класс точности прибора (указан на шкале).

Абсолютная погрешность прибора в любом месте шкалы

                                (4)

где К - класс точности прибора.

Какова же будет погрешность  косвенного определения удельного сопротивления по результатам прямых измерений величин, входящих в формулу (2)?

Известно, что для нахождения среднего значения функции, например y = f(x, z), нужно вычислить ее значение в точках  С учетом этого, используя среднее значение удельного сопротивления в виде найдем относительную погрешность

                       (5)

Отсюда

.                            (6)

Погрешности в определении r, определенные формулами (5) и (6), представляют собой верхний предел систематических и случайных ошибок. Но погрешности, рассчитанные на основании указанных правил, могут быть неоправданно завышенными.

Считается, что если погрешности прямых измерений каждой из определяемых величин (в нашем случае I, U, l и d) независимы, случайны и подчиняются нормальному закону распределения, то более реалистичной (и меньшей) оценкой окончательной погрешности результата измерения является средняя квадратичная ошибка s.

В нашем случае при прямых однократных измерениях I, U и l за среднюю квадратичную ошибку принимается погрешность прибора. Результаты прямых многократных измерений диаметра проволоки будут иметь среднюю квадратичную ошибку

.                                          (7)

При косвенных измерениях (в нашем случае измерение r) средняя квадратичная погрешность вычисляется по формуле:

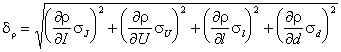 .                      (8)

где  - частная производная функции r(I, U, l, d) по каждой из переменных, рассчитанная по средним значениям прямых

измерений:

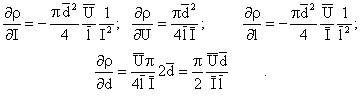
                   (9)

Несложно убедиться, что в результате подстановки выражений (9) в уравнение (8) получим