Изучение температурной зависимости коэффициента внутреннего трения жидкости, страница 2

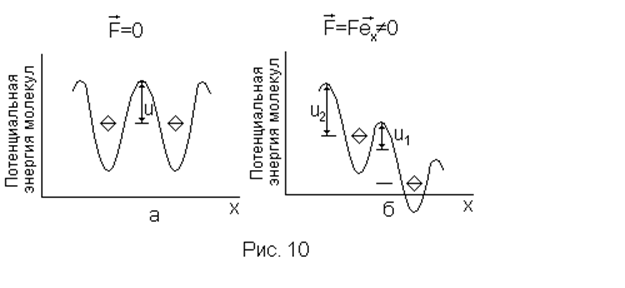
Формуле (37) можно придать определенный физический смысл. При низких температурах вязкость жидкости определяется в основном межмолекулярным взаимодействием и велика по сравнению с вязкостью газов. При нагревании жидкости все большее  число молекул будет преодолевать в единицу времени силы межмолекулярного взаимодействия, становиться на некоторое время “свободными” и более похожими на молекулы газа - вязкость будет уменьшаться. Чтобы понять механизм возникновения вязкости в сложных жидкостях, рассмотрим качественную картину потенциальной энергии молекул, представленную на рис. 10а, где молекулы изображены в виде ромбиков.

Поглощая тепловую энергию kT  порядка величины потенциального барьера U, та или иная молекула может стать на некоторое время “свободной”. Среднее по времени значение вектора скорости  такой молекулы равно нулю - нет выделенного направления движения. Действие внешней силы  на молекулы какого-либо слоя вызывает несимметричные искажения потенциальных барьеров, что приводит к преимущественному направлению перескока молекул. Как видно из рис.10б, молекула будет двигаться преимущественно вдоль оси Х, так как потенциальный барьер U₁<U₂. Импульс направленного движения будет передаваться в другие соседние слои жидкости, на которые силы непосредственно не действуют.

Впервые константа U в формуле (37) интерпретировалась как высота потенциального барьера, который необходимо преодолевать молекуле при переходе из одного состояния в другое (энергия активации молекулы), советским физиком Я.И. Френкелем.

Единицы вязкости.

Как следует из закона Ньютона (36), вязкость определяется как сила сдвига на единицу площади, деленная на модуль градиента скорости. Поэтому размерность вязкости

cила_* время          или                масса  

(длина)_*(длина)                               длина_*время

Используются обе размерности, хотя в большинстве научных работ вязкость выражают в пуазах, сантипуазах, микропуазах и т.д. 1 Пуаз (П) означает вязкость 1 дин·с/см² или 1 г/(с·см), а 1 сП = 1/10² П. В системе СИ вязкость измеряется в Н·с/м² или кг/(с·м). Очевидно, что имеет место соотношение

1 Н·с/м² = 1 кг/(с·м) = 1 Па·с = 10 П

Здесь учтено, что 1 Н/м² = 1 Па (Паскаль).

Вязкость обычных, не очень вязких жидкостей, имеет порядокПа·с, вязкость воды при 20⁰ С равнаПа·с.

Описание установки.

Капиллярный вискозиметр (рис.11) представляет собой капиллярную трубку 5 с измерительным резервуаром 4, ограниченным двумя метками М₁ и М₂. Капиллярная трубка 5 впаяна внутрь корпуса 6 вискозиметра, имеющего два отвода 8 и 9, которые соединяются резиновыми трубками с термостатом. К вискозиметру прилагается насадка 1 с краном 2. Насадка соединяется конусом 3 с корпусом. Нагреваемая в термостате вода прокачивается насосом через корпус вискозиметра. Благодаря этому нагревается капиллярная трубка и исследуемая жидкость.

В вискозиметре используется трубка малого диаметра

(капиллярная трубка) по следующей причине. Под действием внешних сил движение жидкости в трубке может быть как ламинарным, так и турбулентным. При ламинарном движении работа внешних сил расходуется главным образом на преодоление вязкого трения. Распределение скоростей в ламинарном режиме показано на рис.12а. Распределение скоростей при движении жидкости при той же величине внешней силы, но в трубе большего диаметра показано на рис. 12б. Такой режим движения называется турбулентным.

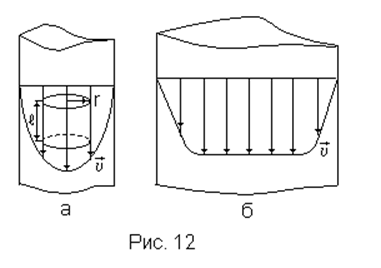
При турбулентном течении жидкости работа внешних сил расходуется как на преодоление вязкого трения, так и на увеличение кинетической энергии жидкости. Математически наиболее просто описать ламинарный режим движения. Поэтому в вискозиметрах используются трубки малого диаметра.

Вывод расчетной формулы для вязкости.

Для получения расчетной формулы воспользуемся тем обстоятельством, что при ламинарном движении силы внутреннего трения между слоями равны внешней силе (в качестве внешней силы в капиллярном вискозиметре используется сила тяжести):

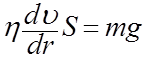.                                         (38)

Представив массу жидкости в виде m=rV=rpr², площадь соприкасающихся слоев в виде S=2pr, где r и V соответственно плотность и объем жидкости в произвольно выбранном цилиндре длиной и радиусом r (см. рис.12а), формулу (38) перепишем в виде

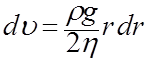.                                             (39)

Интегрирование выражения (39) в пределах от r до R, где R - радиус капилляра, дает зависимость скорости движения слоев от радиуса: