Построение динамических моделей плоских рычажных механизмов. Вариант 2, страница 2

Уравновешивающий момент пар сил:

Задание 2.

Чтобы построить динамическую модель для динамического анализа, используем аналогичные рассуждения как для задания 1.

Для построения динамической модели динамического анализа, используем энергетический метод согласно которого для сохранения эквивалентности модели, все силовые факторы, действующие на подвижные звенья механизма, можно заменить одной силой, которая называется приведенной.

Наличие данной силы является причиной появления приведенного момента пар сил:

,                                                 (8)

где      - длина звена приведения (длина кривошипа), м.

Используя теорему В.И. Жуковского, и выражение (7) найдем значение приведенной силы.

где     - длина отрезка, изображающего плечо на плане скоростей 94,6мм:

          - длина звена приведения 50мм.

 не включено в уравнение т.к. вектор действия этой силы проходит через полюс плана.

Приведенная сила:

 Приведенный момент пар сил:

В общем случае приведенная масса характеризуется следующим выражением:

,                                               (9)

где       , - постоянная и переменная части приведенной массы.

Постоянная часть приведенной массы:

,                                         (10)

где       ,,- приведенные массы энергетической машины, преобразующего устройства и ведущего звена плоского рычажного механизма рабочей машины.

Условиями лабораторной работы величины , не заданы, следовательно их значения приравниваем к нулю.

Выражение (10) примет вид:

                               

Переменная часть приведенной массы:

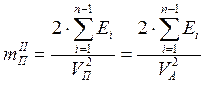,                                  (11)

где      - линейная скорость звена приведения (кривошипа);

           - сумма кинетических энергий развиваемых приводимыми звеньями механизма;

            n – количество подвижных звеньев механизма.

  Сумма кинетических энергий развиваемых приводимыми звеньями механизма:

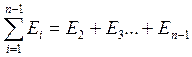,                                    (12)

Кинетическая энергия каждого приводимого звена механизма выражается через кинематические параметры.

В данном механизме звено 2 (ползун) и звено 3 (кулиса) совершают поступательное движение, следовательно, кинетические энергии можно представить в виде:

Кинетическая энергия ползуна:

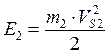,                                                  (13)

Кинетическая энергия кулисы:

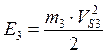.                                                  (14)

где    ,  - линейные скорости центров масс приведенных звеньев, являющихся кинематическими параметрами.

Кинематические параметры механизма выражаются через элементы планов скоростей.

Линейная скорость центра масс ползуна, м/с:

,                                              (15)

Линейная скорость центра масс кулисы м/с:

,                                              (16)

где      , - отрезок на плане скоростей, изображающий вектор ускорения, соответственно, звена 2 и звена 3.

            - масштабный коэффициент плана скоростей

Линейная скорость звена приведения, м/с:

 ,                                        (17)

Преобразуем формулу (12) с учетом формул (13), (14), (15), (16) получим:

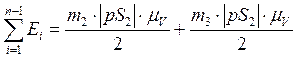
Полученное выражение подставим в формулу (11) с учетом (17):

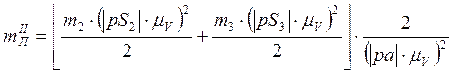
Сокращаем:

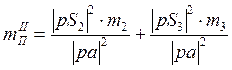,                                     (18)

где      - можно представить в виде ;

             - можно представить в виде k₂.

Формулу (18) можно прелставить в общем виде:

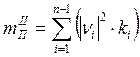,                                                    (19)

 

где        - отрезки изображающие вектора скоростей в составе плана скоростей;

             - коэффициент учитывающий значения постоянных параметров i-ого звена механизма.

 Переменная часть приведенной массы:

=85мм;

=85мм;

=50мм;

=14,43кг;

=24,05кг;

.

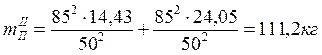Приведенная масса определяется по выражению (9):

Приведенная масса является причиной появления приведенного момента инерции:

,                                                   (20)

Задание 3.

Общее:

1. обе динамические модели составляются с помощью общего метода приведения.

2. данные модели имеют общий силовой динамический параметр, т.е. силы тяжести.

Различия:

1. в каждой модели используется свой метод обеспечения эквивалентности системы:

          - для 1-ой кинетостатический;

          - для 2-ой энергетический.

2. 1-ая модель находится равновесия, а 2-ая в движении.

Вывод:

Обе модели решают одну задачу, определение уравновешивающего момента и силы.