




31)Понятие «датчик» моделирования
При исследовании сложных технических систем методом имитационного моделирования существенное внимание уделяется учету случайных факторов. Так при моделировании эксплуатационной надежности необходимо учитывать такие случайные факторы как условия эксплуатации, наработки на отказ элементов, время и стратегии восстановления работоспособности (замена на новую деталь, замена на отремонтированную деталь, ремонт) отказавших элементов. Для описания действия этих факторов используются «датчики» случайных событий и величин. «Датчики» представляют собой подпрограмму, которая воспроизводит закономерности появления случайных событий и величин реального процесса. На вход «датчика» поступает случайное число, как правило, равномерно распределенное на интервале (0, 1]. На выходе «датчика» генерируется случайная величина, распределенная в соответствии с заданным законом распределения, либо случайное событие, заданное в виде: «0» — событие не произошло, «1» — событие произошло.
Механизм генерирования «датчиком» случайной величины зависит от реализованного метода моделирования, но так или иначе «датчиком» используется либо функция распределения (иногда называемая интегральной функцией распределения) F(х) случайной величины Х, либо плотность распределения (ее иногда называют дифференциальной функцией распределения) f(х). Таким образом для моделирования случайной величины Х необходимо определить функцию распределения F(х) или плотность распределения f(х).
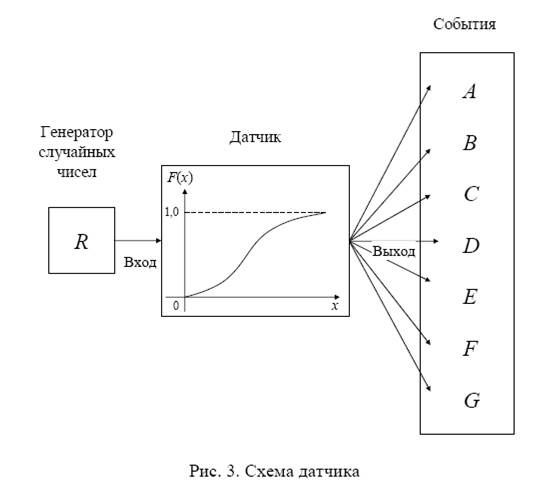
32) Метод обратных функций.
Пусть нужно смоделировать случайную величину Х с плотностью распределения f(х). Интегральная функция распределения случайной величины Х обозначим через F(х), т. е.
![]()
Если
y
–
непрерывная возрастающая функция от z, например y = g(z), то можно
выразить и z
как функцию
от y
с помощью
уравнения z
= g-1(y). Интегральная функция
распределения F(х) – непрерывная возрастающая
функция, а существующая обратная ей функция обозначается через ![]() Значение х случайной величины Х является решением уравнения
Значение х случайной величины Х является решением уравнения
![]()
где
r
– значение
случайной величины R, т. е.![]()
Рассмотрим пример. Пусть случайная величина Х имеет показательный
(экспоненциальный) закон распределения
![]()
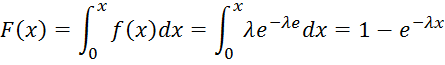
где λ – параметр распределения.
Чтобы найти формулу для моделирования случайной
величины Х
с помощью
равномерно распределенной случайной величины ![]() нужно определить обратную по отношению к F функцию
нужно определить обратную по отношению к F функцию
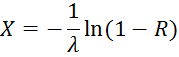
Так
как ![]() имеет то же самое распределение, что и R, то удобнее при нахождении
значений случайной величины Х пользоваться формулой
имеет то же самое распределение, что и R, то удобнее при нахождении
значений случайной величины Х пользоваться формулой
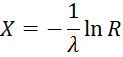
Тогда случайные числа с показательным (экспоненциальным) распределением будут вычисляться по формуле
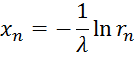
33) Метод отбора или метод Неймана.
Метод отбора для моделирования случайной величины предложен Дж. Нейманом, поэтому в литературе он называется также методом Неймана. Кроме этого встречаются термины: «метод отказов», «метод элиминации». Все эти названия отражают сущность метода: из области задания случайной величины Х отбирается точка с координатами, являющимися функциями случайных чисел с равномерным распределением; если эта точка не может быть использована для расчета Х, то она исключается и отбирается новая. Однако метод отбора применим для получения реализаций только таких случайных величин, закон распределения которых может быть задан с помощью функции плотности.
Рассмотрим моделирование этим методом одномерной случайной величины Х, определенной на интервале (a, b), с плотностью f(x). Вне этого интервала f(x) = 0, и, кроме того, плотность распределения ограничена сверху, т. е. f(x) ≤ с, где с — постоянная. Процедура получения значений случайной величины Х заключается в следующем:
1) получаем два независимых значения r1 и r2 случайной величины R с равномерным распределением на интервале (0, 1];
2) строим точку с координатами ![]()
3) если ![]() , то полагаем, что случайная величина Х приняла значение
, то полагаем, что случайная величина Х приняла значение ![]() ; если
; если ![]() , то точка
, то точка ![]() исключается и вычисления повторяются с получением новой пары
случайных числе {rn} по пункту 1.
исключается и вычисления повторяются с получением новой пары
случайных числе {rn} по пункту 1.
Полученные таким образом значения являются реализациями случайной величины Х с плотностью f(x).
Эффективность метода отбора называют вероятность того,
что точка ![]() будет использована для расчета Х. Поэтому ясно, что при
большом числе отброшенных точек метод отбора неэффективен. В рассмотренном выше
случае, когда Х
определена
на интервале (a, b), эффективность метода
характеризуется отношением площади, ограниченной кривой f(x), осью х, прямыми х = а и х = b, к площади прямоугольника c(b – a)
будет использована для расчета Х. Поэтому ясно, что при
большом числе отброшенных точек метод отбора неэффективен. В рассмотренном выше
случае, когда Х
определена
на интервале (a, b), эффективность метода
характеризуется отношением площади, ограниченной кривой f(x), осью х, прямыми х = а и х = b, к площади прямоугольника c(b – a)
34) Принцип построение алгоритмов имитационного моделирования.
Существует три принципа построение имитационных алгоритмов: принцип Δt, принцип особых состояний и принцип последовательной проводки заявки. С целью повышения эффективности имитационных алгоритмов сложных систем иногда используют комбинацию принципов моделирования.
Алгоритм имитационного моделирования эксплуатационной надежности автомобиля использует принцип особого состояния. Под особым состоянием понимается отказ, ремонт, техническое обслуживание. Процесс формирования последствий отказ можно имитировать на основе последовательной проводки заявки (например, время восстановления элемента, вид отказа)
Принцип Δtоснован на отслеживании параметров системы через равные интервалы времени. Преимуществом указанного принципа является его универсальность. Алгоритмы, построенные на его основе, отличаются простотой организации связей между структурными составляющими моделями. По этой причине при использовании принципа Δt практически не возникает ограничений, связанных со сложностью(размерами) исследуемой системы. По этому принцип Δt нашел широкое применение при разработке имитационных алгоритмов. Указанный принцип используется в методе автоматного моделирования, в некоторых языках программирования.
Принцип особых состояний(от события к событию) является более экономным по времязатратам на работу ЭВМ по сравнению с принципом Δt. Он заключается в следующем. По известным параметрам предыдущих особых состояний(событий) на каждом шаге моделирования определяется интервал квантования. Таким образом, в момент каждого последующего просмотра параметров система приходит в особое состояние. Это и обусловливает относительно небольшие затраты времени на работу ЭВМ при моделировании.
Недостаток: при увеличении количества элементов системы повышаются затраты времени на определение момента перехода в следующее особое состояние.
Принцип последовательной проводки заявки. Основным преимуществом алгоритмов, использующих такой принцип, является минимальные времязатраты на работы ЭВМ по сравнению с алгоритмами, в которых применяются принципы, рассмотренные выше. Однако алгоритмы на основе принципа последовательной проводки заявки отличаются большой сложностью, что обусловливает значительные затраты ресурсов на их разработку и программную реализацию.
35) методичка стр 44 рис14
36) методичка стр 67 рис 23
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.