Корреляционный анализ спроса

Министерство образования и науки РФ

Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Политехнический институт

Кафедра "Транспорта"

Практическая работа № 1

Корреляционный анализ спроса

Преподаватель                         __________              Терских В.М.

Студент  ФТ 10-07                  __________              Байрамуков В.Ю.

Красноярск 2014г.

Заданиена практическую работу:

Вариант 27

Исходные данные

Номенклатура	Месяц
	1	2	3	4	5	6	7	8	9	10	11	12
k	15	7	13	8	9	11	8	10	8	15	7	8
l	14	14	9	11	12	14	8	8	10	16	6	6
m	10	6	9	8	9	8	7	10	5	12	3	5
n	1	3	3	3	2	2	5	4	3	1	6	5
h	12	4	12	10	9	11	8	11	3	13	1	7

Ход работы

Часть 1. Коэффициент корреляции

Заданы продажи пяти номенклатур ( k, l, m, n, h) запасной части в магазине в течение 12 месяцев. Требуется определить существует ли линейная зависимость между продажами данных номенклатур.

Сперва определим связь для k-й (в расчете i-й) и l-й (в расчете j-й) номенклатур.

Для этого расчет производим в следующем порядке.

1.  Определяем среднее значение спроса по i-й и j-й номенклатуре запасных частей:

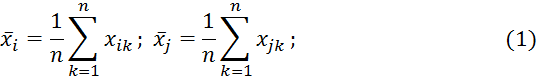
2.  Далее находи эмпирические дисперсии:

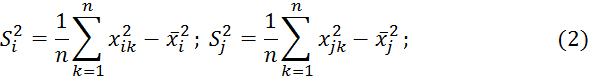
3.  Вычисляем эмпирическую ковариацию:

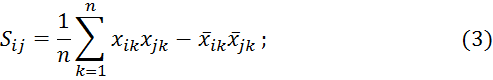
4.  Рассчитываем коэффициент корреляции:

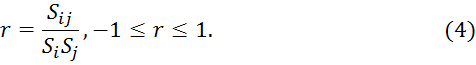
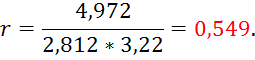
5.  Аналогично производим расчет для остальных сочетаний номенклатур и получившиеся коэффициенты корреляции сводим в таблицу 1.

Таблица 1

6.  Построим диаграммы рассеивания для сочетаний номенклатур, для которых

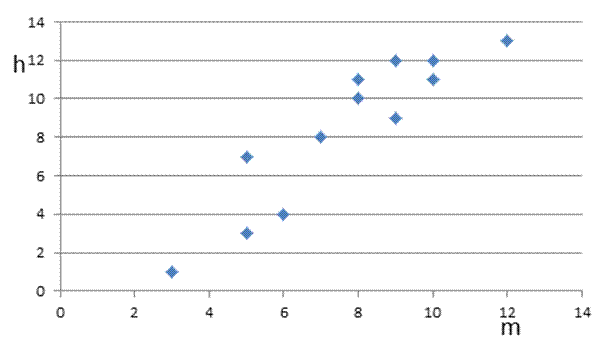
Рис 1. Диаграмма рассеивания для mhсочетания, 

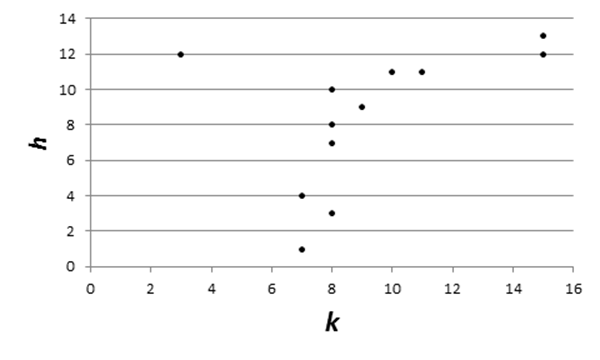
Рис 2. Диаграмма рассеивания для khсочетания,

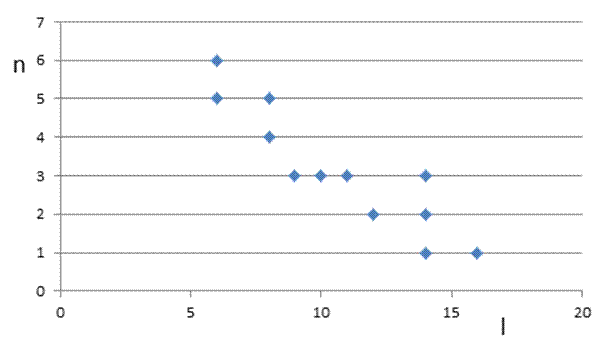
Рис 3. Диаграмма рассеивания для lhсочетания,

На основании полученных расчетов делаем следующие выводы.

Чем ближе rк нулю, тем слабее корреляция. И наоборот, чем ближе к 1 или  -1, тем сильнее корреляция, т.е. зависимость между номенклатурами близка к линейной.

Часть 2. Корреляционное отношение

1.  Определим корреляционное отношение спроса на номенклатуру h от k спроса на номенклатуру согласно варианту задания. Для этого сгруппируем данные и представим их в виде таблицы 2.

Таблица 2

Середина интервала		Середина интервала xi													nxi	x среднее
		x1	x2	x3	x4	x5	х6	x7	x8	x9	x10	x11	x12	x13
		1	2	3	4	5	6	7	8	9	10	11	12	13
yi1	15												1	1	2	12,5
yi2	14														0	0
yi3	13												1		1	12
yi4	12														0	0
yi5	11											1			1	11
yi6	10											1			1	11
yi7	9									1					1	9
yi8	8			1				1	1		1				4	7
yi9	7	1			1										2	2,5
nyi		1	0	1	1	0	0	1	1	1	1	2	2	1	12	8,42
y среднее		7	0	8	7	0	0	8	8	9	8	10,5	14	15	9,92	—

Расчёт корреляционного отношения  целесообразно начинать с расчёта суммы:

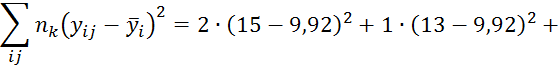
Для нахождения суммы вычислим её сначала для каждого i (для каждого столбца таблицы 1) и результаты сложим.

При i=1

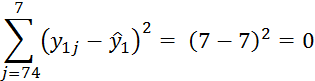
При i=2

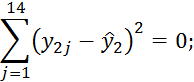
При i=3

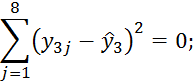
При i=4

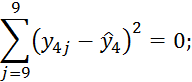
При i=5

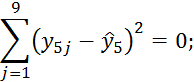
При i=6

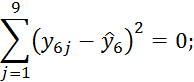
При i=7

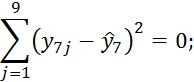
При i=8

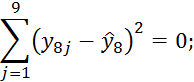
При i=9

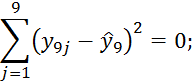
При i=10

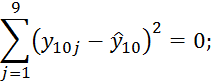
При i=11

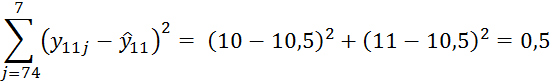
При i=12

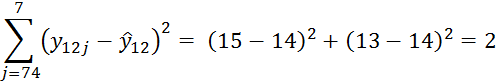
При i=13

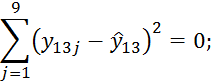
Суммируя все эти значения, получим

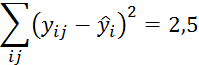
В результате значение корреляционного отношения

2.  Построим диаграмму рассеивания

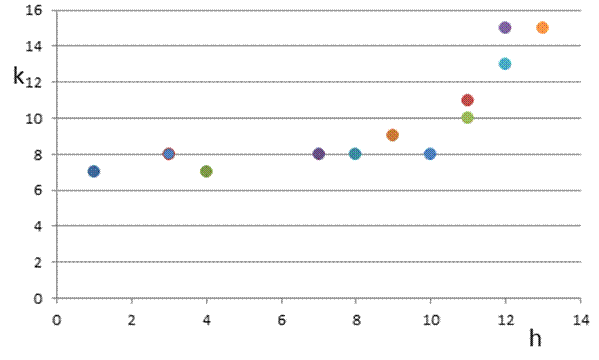
Рис 4. Диаграмма рассеивания для hот k.

Коэффициент корреляции для диаграммы рассеивания, показанной на рис. 4, , т. е. коэффициент корреляции близок к нулю. Также рассчитанное корреляционное отношение для этого сочетания получилось больше коэффициента корреляции и близко к единице, отсюда следует, что в данном случае присутствует  некоторая зависимость между X и Y..

3.  Теперь аналогично рассчитаем корреляционное отношение для зависимости kот h. И также построим диаграмму рассеивания.

В результате значение корреляционного отношения получилось

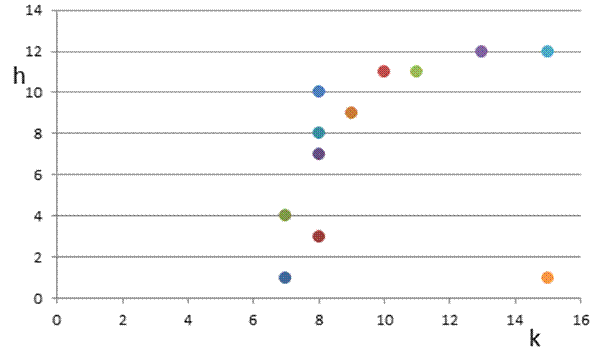
Рис 5. Диаграмма рассеивания для kот h.

Итак, делаем вывод, что при помощи коэффициента корреляции нельзя выявить нелинейную зависимость. Если связь между X и Y нелинейная, то необходимо использовать корреляционное отношение. В данном случае значение корреляционного отношения близко 0, что свидетельствует о наличии линейной зависимости.

Также получается, что корреляционное отношение несимметрично относительно X и Y, поэтому наряду с , необходимо рассматривать — корреляционное отношение Xпо Y, определяемое аналогичным образом.