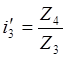Назначение и типы коробок передач, страница 2

.                                                                    (11)

Если общее передаточное число на третьей передаче мы обозначим через ί₃, то:

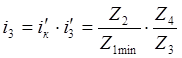.                                                 (12)

Передаточное число между промежуточным и вторичным валами можно записать:

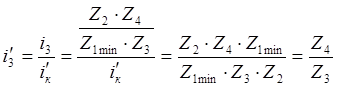.                                 (13)

Величину ί'₃ мы уже можем определить, но числа зубьев Z₃ и Z₄ нам неизвестны и их еще предстоит определить. По аналогии с определением ί'₃ мы можем рассчитать передаточные числа между промежуточным и вторичным валами для всех передач, кроме прямой. Последнее нам определять нет надобности.

Итак, по уравнению (13) мы имеем соответственно для всех передач:

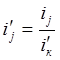,                                                           (14)

где     j – индекс, указывающий номер передачи.

6) Определение числа зубьев шестерен по известным передаточным числам между промежуточным и вторичным валами

Эту операцию проделаем на примере третьей передачи (см. рис. 1), решая два уравнения с двумя неизвестными Z₃ и Z₄:

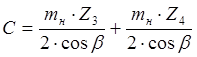,                                                        (15)

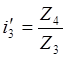.                                                                              (16)

Выразим из (16) Z₄ и подставим в (15):

.

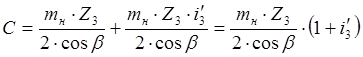Тогда:                    .

Окончательно

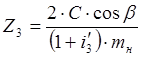.                                                       (17)

Подставляя Z₃ из (17) в (15), получим:

.

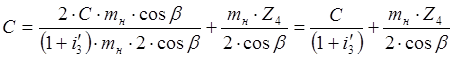Освобождаясь от знаменателей, получаем:

.

И окончательно имеем

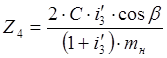.                                                   (18)

Проверка:             .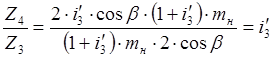

Из сравнения уравнений 17 и 18 видно, что число зубьев Z₄ можно было сразу рассчитать после определения Z₃ из уравнения .

После определения основных параметров шестерен следует рассчитать контактные напряжения между их зубьями шестерен.

4. Расчёт контактных напряжений

Общее выражение для определения напряжений в месте контакта:

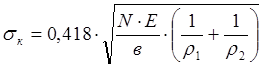.                                             (19)

где     σ_к – контактные напряжения в полюсе зацепления шестерен;

N – нормальное давление между зубьями в полюсе зацепления;

Е – модуль упругости первого рода;

r₁ и r₂ – радиусы кривизны зубьев в полюсе зацепления соответственно ведущей и ведомой шестерен;

в – рабочая длина контакта или ширина шестерни.

Прямозубое зацепление шестерён:

а) Нормальное давление в полюсе зацепления

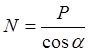.                                                      (20)

где     a - угол зацепления б) Рабочая длина контакта.

Рабочая длина контакта для прямозубого зацепления может быть принята ориентировочно равной ширине шестерни в) Радиусы кривизны в полюсе зацепления.

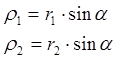.                                                           (21)

где     r₁и r₂ радиусы начальных окружностей ведущей и ведомой шестерни.

Подставляя в (19) выражения (20) и (21) получим выражение для определения контактных напряжений прямозубого зацепления.

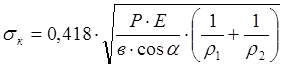.                                          (22)

Косозубое зацепление шестерён:

а) Нормальное давление в полюсе зацепления:

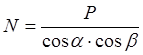.                                                       (23)

где     a – угол зацепления;

b – угол аклона зубьев б) Рабочая длина контакта:

Рабочая длина контакта для косозубого зацепления может быть рассчитана по формуле:

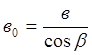.                                                                (24)

где     в – ширина шестерни.

в) Радиусы кривизны в полюсе зацепления:

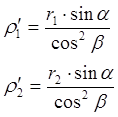.                                                           (25)

где     r₁и r₂ радиусы начальных окружностей ведущей и ведомой шестерни.

Подставляя в уравнение (19) выражения (23), (24) и (25) получим выражение для определения контактных напряжений косозубого зацепления.

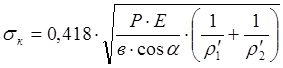.                                          (26)

В формулах (20) и (21) Р – это окружное усилие на начальной окружности.

Для первичного вала:

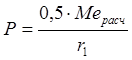.                                                         (27)

Для вторичного вала:

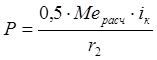.                                                     (28)

где     Ме_расч – расчётный крутящий момент;

i_к – передаточное число коробки передач для рассчитываемой передачи.

.                                                    (29)

где     Ме_max – максимальный крутящий момент двигателя.

Допускаемые контактные напряжения в зацеплении.

Шестерни	[σк], МПа
	Цементируемые	Цианируемые
I перед. и 3Х	1900 – 2000	950 – 1000
Постоянное зацепление и высшие передачи	1300 – 1400	650 - 700

Прогиб вторичного вала:

0,13 – 0,15 мм для высших передач

0,15 – 0,25 мм для низших передач

Валы КП передают крутящий момент и испытывают изгиб под действием сил, действующих в зубчатых зацеплениях.

Окружная сила:

Радиальная сила:

Осевая сила:

где  – передаточное число до рассчитываемой шестерни;

 – диаметр шестерни;

 – крутящий момент, приложенный к первичному валу.

 – угол зацепления;

 – угол наклона зубьев шестерён.