Определение параметров цепей при гармоническом режиме колебаний, страница 2

Решение:

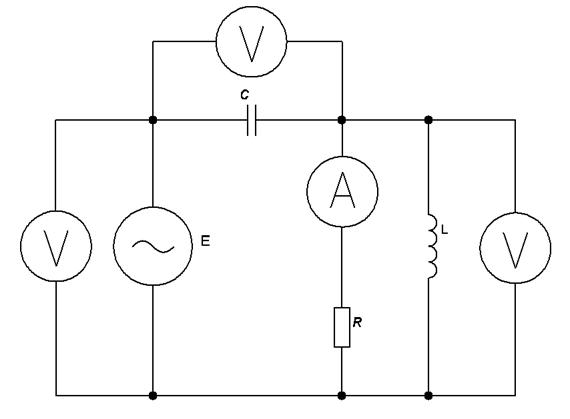
Так как величины всех напряжений в схеме равны, то при сложении на векторной диаграмме они будут составлять равносторонний треугольник. Следовательно, разность фаз между напряжением на активном сопротивлении и на емкости составляет угол . Комплексы действующих значений будут иметь вид:

По закону Кирхгофа для напряжений определим комплекс действующего значения напряжения :

Вектор тока  и вектор напряжения  совпадают с направлением вектора напряжения . Вектор тока  отстает от вектора напряжения  на , а вектор тока  опережает вектор напряжения  на . Следовательно сумма токов на векторной диаграмме будет составлять равнобедренный треугольник, катетами которого являются вектора  и , а гипотенузой . Из выше сказанного также можно сделать вывод, что угол между векторами  и  составляет . Исходя из этого найдем величину тока протекающего через емкость и величину тока протекающего через индуктивность.

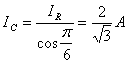
Зная величину углов, запишем комплексы действующих значений этих токов:

Определим сопротивления элементов:

Общее сопротивление схемы можно найти по формуле:

Отобразим векторную диаграмму для данной схемы, на которой нанесем все токи и напряжения:

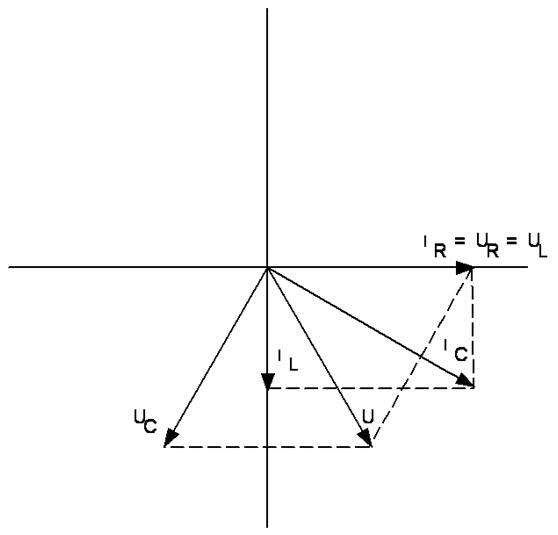
Задача 3: Цепь в синусоидальном режиме. Определить , , , ,  и проконтролировать баланс мощностей.

Дано: 121 – ИТ, ; 212 – ; 312 – ; ; ; .