Федеральное агентство по образованию
Государственное учреждение высшего профессионального образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Политехнический Институт
Кафедра: «Автомобили и Двигатели»
ПРАКТИЧЕСКАЯ РАБОТА №3
Расчет дифференциала
автомобиля ВАЗ-2105
Выполнил: студент АТ 64-1
Мутовина А.И.
Проверил: Муромцев А. С.
Красноярск 2007
Дифференциал – механизм трансмиссии автомобиля, распределяющий подводимый к нему крутящий момент между выходными валами и обеспечивающий их вращение с разными угловыми скоростями.
Дифференциалы по конструкции разделяют на шестеренчатые, кулачковые, червячные и с механизмами свободного хода.
Наибольшее распространение получили конические шестеренчатые дифференциалы, обладающие большей компактностью в сравнение с цилиндрическими. Недостатком конических дифференциалов является наличие осевых усилий и большое трение на торцах конических шестерен.
Исходные данные:
автомобиль прототип – ВАЗ 2105, ![]() , остальные параметры
приведены в таблице 3.
, остальные параметры
приведены в таблице 3.
Таблица 3 Геометрические параметры зубчатых колес конического симметричного дифференциала автомобиля ВАЗ-2105.
|
Автомобиль |
Число зубьев |
Внешний окружной модуль, мм |
Конусное расстояние или длинна образующего конуса, мм |
Угол профиля (угол зацепления), град |
Ширина венца, мм |
Число сателлитов |
|
|
Сателлитов |
Шестерен |
||||||
|
ВАЗ 2105 |
10 |
16 |
4,00 |
37,77 |
22°30¢ |
12,0 |
2 |
Нормальный модуль:
![]() (10), где
(10), где ![]() - окружной модуль,
- окружной модуль,
![]() - половина угла при
вершине начального конуса сателлита,
- половина угла при
вершине начального конуса сателлита,
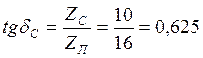 ,
,
![]() ,
,
![]() ,
,
Примем нормальный модуль ![]() .
.
Длину образующей конуса примем
как у прототипа ![]() .
.
Длина зуба:
![]() ,
,
Коэффициент блокировки принимаем
из таблицы 4; ![]() 5.
5.
Таблица 4. Коэффициенты блокировки дифференциалов.
|
Тип дифференциала |
Коэффициент блокировки |
|
Шестеренчатые дифференциалы |
0,05-0,15 |
|
Самоблокирующиеся кулачковые дифференциалы |
0,3-0,5 |
|
Самоблокирующиеся червячные дифференциалы |
0,8 |
|
Шестеренчатые дифференциалы с принудительной блокировкой |
0-0,78 |
|
Дифференциалы с механизмами свободного хода |
1,0 |
Коэффициент ![]() :
:
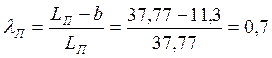 ,
,
Половина угла при вершине образующего конуса полуосевой шестерни:
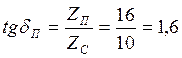 ,
,
![]() ,
,
Приведенное число зубьев полуосевой шестерни:
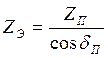 (11),
(11),
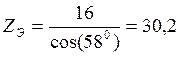 ,
,
По ![]() и
и ![]() из таблицы 2 находим коэффициент формы
зуба
из таблицы 2 находим коэффициент формы
зуба ![]() .
.
Напряжения изгиба у основания зуба полуосевой шестерни:
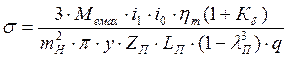 (12), где
(12), где ![]() - максимальный момент, развиваемый
двигателем,
- максимальный момент, развиваемый
двигателем,
![]() - передаточное число
коробки на низшей передаче,
- передаточное число
коробки на низшей передаче,
![]() - передаточное число
главной передачи,
- передаточное число
главной передачи,
![]() - КПД трансмиссии,
- КПД трансмиссии,
![]() - коэффициент
блокировки дифференциала,
- коэффициент
блокировки дифференциала,
![]() - нормальный модуль,
- нормальный модуль,
![]() - коэффициент формы
зуба,
- коэффициент формы
зуба,
![]() - число зубьев
полуосевой шестерни,
- число зубьев
полуосевой шестерни,
![]() - длина образующей
начального конуса полуосевой шестерни,
- длина образующей
начального конуса полуосевой шестерни,
![]() - число сателлитов.
- число сателлитов.
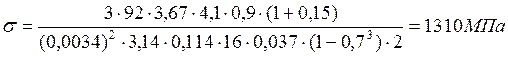 ,
,
Допускаемое напряжение ![]() . Превышение составляет 2,4 раза.
. Превышение составляет 2,4 раза.
Подобное превышение допустимо по следующим причинам:
1) вышеприведенная методика является приближенной и дает завышенные величина напряжений;
2) превышение напряжений имеет место лишь на первой передаче, на второй передаче напряжения будут превышать допустимые на 45%, на третьей- на 7%,на четвертой напряжения уже будут значительно ниже допустимых ;
3) небольшие скорости полуосевых шестерен и сателлитов при движении на первой и второй передачах обеспечивают режим их работы, близкий к статическому.
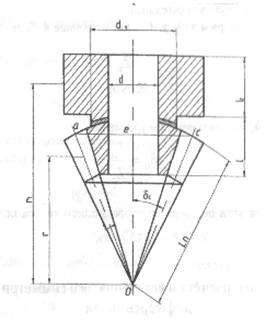
 Рис. 4. Расчетная
схема сателлита.
Рис. 4. Расчетная
схема сателлита.
Определим уточненный торцевой модуль:
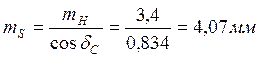 ,
,
Зная торцовый модуль, рассчитаем диаметр наружной окружности сателлита по большому конусу:
![]() ,
,
Полученный диаметр является
основанием ![]() (см. рис. 4) равнобедренного треугольника
(см. рис. 4) равнобедренного треугольника ![]() , стороны которого являются образующими
сателлита.
, стороны которого являются образующими
сателлита.
Половина диаметра ![]() вместе с конусным расстоянием
вместе с конусным расстоянием ![]() , образуют прямоугольный треугольник, высоту
которого
, образуют прямоугольный треугольник, высоту
которого ![]() можно определить по теореме Пифагора:
можно определить по теореме Пифагора:
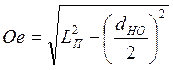 (13),
(13),
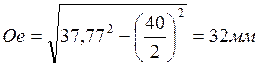 ,
,
Высота ножки зуба:
![]() ,
,
Принимаем размеры, исходя из
прототипа: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Удельное давление на опорную поверхность оси сателлита в шестерне:
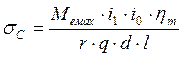 (14),
(14),
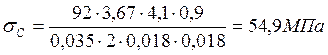 ,
,
Удельное давление на ось сателлита в месте закрепления ее в коробке дифференциала:
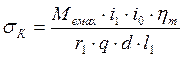 (15),
(15),
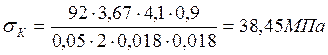 ,
,
Удельное давление по торцу сателлита:
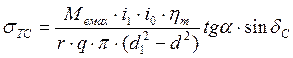 (16),
(16),
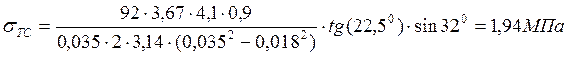 .
.
Расчетные удельные давления ни в
одном случае не превышают допустимых ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.