Расчет суммы получения клиентом при закрытии счета, применив французский способ определения сроков хранения вкладов. Сравнение величины дохода на заданную сумму при начислении сложных процентов

Содержание

Задача 1.3. 3

Задача 2.3. 4

Задача 3.3. 5

Задача 4.3. 6

Задача 5.3. 8

 

Задача 1.3

При открытии счета 03.04 в банке по ставке 11,5% годовых было внесено 10 тыс. руб. Затем 15.06 было снято 3 тыс. руб., а 05.09 вновь внесено 5 тыс. руб. Определить сумму, которую получит клиент при закрытии счета  01.11, применив французский способ определения сроков хранения вкладов.

Решение

Начисление процентов осуществляется при помощи формулы:

, где PV – первоначальная сумма денег,

i – ставка процента,

k – количество дней начисления процентов.

При определении расчетного количества дней примем французский способ, т.е. 360 дней в году, количество дней в месяцах равным их фактической календарной длительности.

Срок хранения 10000,00 рублей составил:

k1= 28+31+15-1 = 73 дня

Срок хранения 7000,00 рублей составил:

k2= 15+31+31+5-1 = 81 день

Срок хранения 12000,00 рублей составил:

K3= 25+31+1-1 = 56 дней.

Сумма начисленных процентов:

I= (10000,00*73 + 7000*81 + 12000*56)0,115/360 = 634,80 рублей

Сумма полученная при закрытии счета:

PV= 12000,00 + 634,80 = 12634,80 рублей.

Ответ:  сумма при закрытии счета составит 12634,80 рублей.

Задача 2.3

Сравните величины дохода, если на сумму 20 тыс. руб., инвестированную на 3 год, начисляются сложные проценты по ставке 9% годовых: а) ежегодно, б) по полугодиям, в) ежеквартально, г) ежемесячно.

Решение

Определим будущую сумму при разном способе начисления процентов при помощи формулы:

, где PV – первоначальная сумма денег,

i – ставка процента,

n – число периодов.

Определим искомые суммы:

а)  руб.

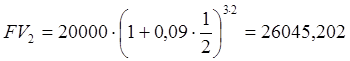б)  руб.

в) 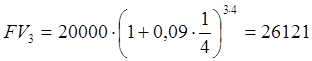 руб.

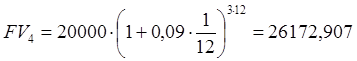г)  руб.

Ответ: ежегодная величина дохода – 5900,58 руб.; за полугодие - 6045,20 руб.; за квартал - 6121 руб.; за месяц - 6172,91 руб.

Задача 3.3

Банк начисляет на вложенные в него деньги проценты по ставке 5% за квартал. Какую ставку непрерывных процентов должен установить банк,  чтобы доходы клиентов не изменились?

Решение

Определим ставку непрерывных процентов при помощи формулы:

где i – процентная ставка,

 - ставка непрерывных процентов.

= ln (1+ 0,05)=ln 1,05 = 0,04879; = 4,88%

Ответ: в банк нужно установить  ставку непрерывных процентов равную 4,88%.

Задача 4.3

Кредит 600 тыс. руб. выдан на 5 лет под 18% годовых (простых). По договору заемщик должен вернуть 200 тыс. руб. через 2 года и такую же сумму еще через 2 года. Определите величину последней выплаты двумя способами: а) по правилу торговца; б) актуарным методом.

Решение а) Определим проценты по кредиту на весь срок:

, где PV – первоначальная сумма денег,

i – ставка процента,

k – срок начисления процентов.

 руб.

Первая вычитаемая сумма:

 руб.

Вторая вычитаемая сумма:

 руб.

Величина последней выплаты:

1140000-308000-236000=596000 руб.

Заемщик заплатит всего: R1+R2+R3=200000+200000+596000=996000руб.

Стоимость кредита: I=996000-500000=396000 руб.

б) Определим сумму к погашению актуарным методом.

Величина первого остатка долга:

 руб.

После второй выплаты остаток долга составит:

 руб.

Последняя выплата составит:

 руб.

Заемщик заплатит всего: R1+R2+R3=200000+200000+752556,8=1152556,8 руб.

Стоимость кредита: I=1152556,8-500000=552556,8 руб.

Ответ: величина последней выплаты по правилу торговца составит 596000,00 рублей, стоимость кредита составит 396000 рублей; а по актуарному методу величина последней выплаты составит 752556,80 рублей, стоимость кредита 552556,8 рублей.

Задача 5.3

Определить, на какой срок в днях нужно заключить договор, если банковская учетная ставка 20% годовых, клиент хочет получить  25000 руб., обязуясь вернуть 30000 руб.

Решение

Определим срок при помощи формулы:

, где PV – первоначальная сумма,

i – ставка процента,

k – срок начисления процентов.

Имеем:

25000(1+0,2∙k)=30000

1+0,2∙k=30000/25000

0,2k=1,2-1

k=0,2/0,2=1 год

Ответ: нужно заключить договор на 360 дней.