Расчет гидротурбины ПЛ40/587а-46 (расчетный напор - 36,3 м, номинальная мощность турбины одного агрегата - 75000 кВт), страница 6

По сравнению с другими типа турбинных камер они имеют минимальные габариты, обеспечивают осесимметричный подвод потока и необходимую его закрутку, а также позволяют разместить значительную часть гидротурбинного оборудования в защищенном от воды помещении.

Проектирование спиральных камер проводят с учетом следующих требований:

1)  Обеспечение равномерного распределения расхода по окружности направляющего аппарата;

2)  направление потока перед лопатками направляющего аппарата должно быть таким, чтобы на основных режимах работы турбины они обтекались с небольшими углами атаки;

3)  размеры и конфигурация радиальных сечений спиральной камеры должны быть такими, чтобы скорости воды в ней не превосходили некоторых предельных значений, определяемых уровнем допустимых потерь, а также удовлетворяли требованиям общей компоновки здания ГЭС;

4)  обеспечение условий прочности и исключение протечек воды в другие части здания ГЭС.

При напорах Hменьше 40 м спиральные камеры выполняются железобетонными.

Спиральная камера состоит из подводящего канала и спирального канала, характеризуемого углом охвата . Ниже представлены основные параметры спиральной камеры для турбины ПЛ 70.

Таблица 3.1

Основные параметры спиральной камеры для гидротурбины ПЛ 40

Параметр	РО 115
, град	225
	0,375
.	2,7

3.2Гидромеханический расчет бетонной спиральной камеры

1.  Выбираем угол охвата  и высоту направляющего аппарата , задаем размеры входных и выходных кромок статора.

b₁=b₂,

α₁=25°,

α₂=15°.

2.  Определяем расход через турбину

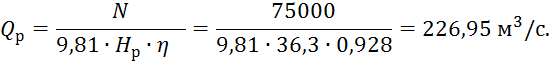
Где значение  турбины определяется по универсальной характеристике турбины в рабочей точке.

Находим расход через входное сечение

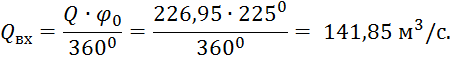
3.  Определяем среднее значение  скорости  во входном сечении спирального канала  и вычисляем площадь входного сечения.

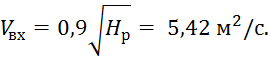
4.  Определяем размеры входного сечения, площадь которого рабна F_вх.

F_вх = (R_вх – r_b)·b_вх + b₀·(r_a – r_b) – (b_вх- b₀)·(tgα₁ + tgα₂)/2

R_вх = 1,6·D₁ = 1,6·5 = 8 м.

b_вх =5,575 м.

5.  Вычисляем интеграл 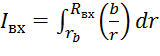 для входного сечения камеры. Для этого площадь входного сечения разбивают на 5 частей, под сечением строят график зависимости (b/r)=f(r) по изменениям b и r каждого элемента (табл. 3.2).

Таблица 3.2.

Площадь фигуры под графиком представляет собой значение интеграла .

6.  Задаем 5 радиальных сечений спирали, определяем 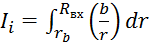. Для этого достраиваем график зависимости (b/r)=f(r) для каждого сечения (табл. 3.3).

Таблица 3.3.

7.  Находим углы  расположения заданных сечений в плане спиральной камеры по формуле:

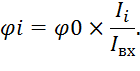
Значения  и  приведены в табл. 3.4.

Таблица 3.4.

8.  По данным таблицы 3.4 строим график , где  – радиусы наружной стенки расчетных сечений (рис.3.1).

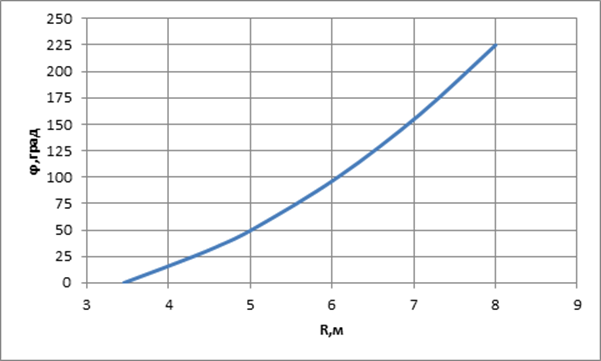
Рисунок 3.1 - Зависимость .

9.  Используя зависимость ., находим значения  через каждые 15 от  до  (табл. 3.5).

Таблица 3.5.