Решение игры в чистых стратегиях и в смешанных стратегиях. Определить оптимальный план продажи товаров, страница 2

Игрок 1 и 2 с применением оптимальных смешанных стратегий улучшают свое положение по отношению нижних и верхних цен игры. Улучшение состоит в том, что игрок 1, придерживаясь своих оптимальных стратегий, овладеет на 0,3% больше выигрыша у игрока 2, чем при реализации максиминной стратегии. В свою очередь, игрок 2 снижает цену игры на 1,7 процентных пункта по сравнению с ценой, достигаемой при минимаксной чистой стратегии.

Если игрок 1 будет применять стратегию А₄ риск будет максимальным, и будет состоять в том, что игрок выиграет меньше 6,3%.

Если игрок 2 будет пользоваться стратегиями В₂, В₃, В₅ то он проиграет больше 6,1%.

Таким образом, оптимальные стратегии 1-го игрока U*= (0,12, 0,04, 0, 0) и 2-го игрока Z*=(0, 0, 0, 0,14, 0,02). Цена игры υ = 0,16.

Задача 2. Розничное торговое предприятие разработало несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей, получающиеся от их возможных сочетаний. Величины прибыли представлены в виде матрицы выигрышей. Определить оптимальный план продажи товаров.

Величина прибыли
План продажи	Состояние конъюнктуры и спроса
	К1	К2	К3	К4	К5
П1	5,6	7,4	7,3	6,2	4,4
П2	3,9	5,7	3,2	4,3	6,1
П3	6,6	4,4	5,8	3,5	7,1
П4	4,5	3,8	6,3	5,9	3,2
П5	7,6	6,4	4,9	7,2	5,1

Решение:

Найдем верхнюю и нижнюю цену игры, проверим игру на наличие седловой точки.

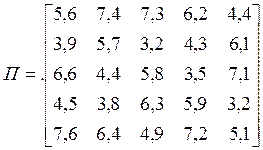
α – нижняя цена игры находится по формуле:

β – верхняя цена игры

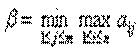
Если верхняя и нижняя граница совпадают, значит их общее значение является седловой точкой, т.е. игра решается в чистых стратегиях.

	К1	К2	К3	К4	К5	min	max
П1	5,6	7,4	7,3	6,2	4,4	4,4	4,9
П2	3,9	5,7	3,2	4,3	6,1	3,2
П3	6,6	4,4	5,8	3,5	7,1	3,5
П4	4,5	3,8	6,3	5,9	3,2	3,2
П5	7,6	6,4	4,9	7,2	5,1	4,9
max	7,6	7,4	7,3	7,2	7,1
min	7,1

α = 4,9

β = 7,1

4,9≠7,1, значит седловой точки нет, значит игра не решается в чистых стратегиях. Компромиссное значение существует, ему соответствует α^*, для которой выполняется неравенство

Составим симметричную пару ЗЛП для плана продаж (П) и состояния рынка (К) соответственно.

Рассмотрим задачу с позиции интересов П. При фиксированных стратегиях К П применяет свои стратегии с вероятностями р₁, р₂, р₃, р₄, р₅

Для фиксированных стратегий К ожидаемый проигрыш П составит:

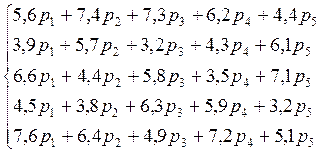
Игрок 1 заинтересован, чтобы проигрыш не превысил α, т.е. справедливы неравенства:

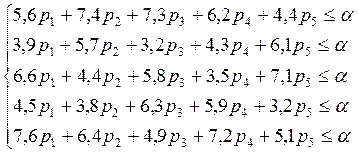
При этом р₁+ р₂+ р₃+р₄+р₅=1

Так как α>0, разделим обе стороны неравенства на α и введем обозначение  

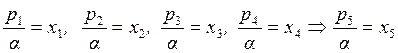
/α

Для игрока 1 α – ожидаемая величина потерь и он заинтересована в снижении этой величины в том, чтобы  тогда 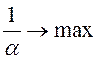. Переходим к системе неравенств:

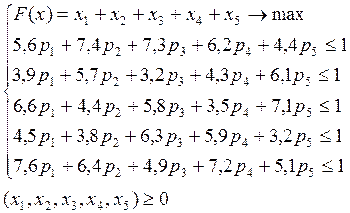
Для фиксированных стратегий К ожидаемый выигрыш П составит:

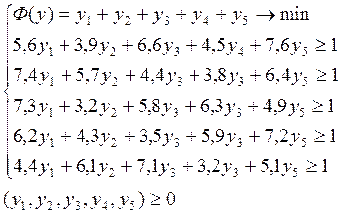
С применением программного пакета MS Excel получаем следующие результаты:

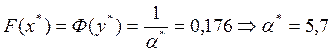 (оптимальный размер выигрыша П и проигрыша К, %). Выполняется требование основной теоремы:

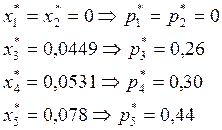
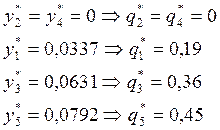
П и К с применением оптимальных смешанных стратегий улучшают свое положение по отношению нижних и верхних цен игры. Улучшение состоит в том, что П, придерживаясь своих оптимальных стратегий, овладеет на 0,8% больше выигрыша у К, чем при реализации максиминной стратегии. В свою очередь, К снижает цену игры на 1,4 процентных пункта по сравнению с ценой, достигаемой при минимаксной чистой стратегии.

Если П будет применять стратегию П₁ или П₅ риск будет максимальным, и будет состоять в том, что фирма выиграет меньше 5,7%.

Если К будет пользоваться стратегией К₁ или К₄, то проиграет больше 5,7%.

Таким образом, оптимальные стратегии П U*= (0, 0, 0,26, 0,30, 0,44) и К Z*=(0,19, 0, 0,36, 0, 0,45). Цена игры υ = 0,176.