Строительство и архитектура \ Инженерная гидрология

Построение интегральной кривой стока в прямоугольной системе координат по среднемесячным расходам реки Долгая. Построение математической и эмпирической кривых обеспеченности по среднегодовым расходам реки Ящера

Страницы работы

11 страниц (Word-файл)

Скачать файл

Фрагмент текста работы

функции не известен, то величина определяется методом суммирования прямоугольников.

3) Тангенс угла наклона (α) прямой проходящей через две точки на кривой стока численно равен среднему расходу за время Δ t_i= t₂-t_1.

tg α =(W₂-W₁)/( t₂-t₁)= Δ W/ Δ t=Q_1-2- средний расход за время от t₁ до t₂

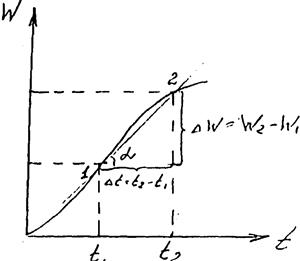
Рис. 2.

4) Если точка 1 стремится к точке 2, то секущая превратится в

касательную, то есть при Δ t —> 0

lim Δ W/ Δ t = tg α =Q₂ - мгновенный расход в точке 2:

5) Средний годовой расход можно получить, соединив прямой точки соответствующие началу и окончанию года.

Все расчеты для построения интегральной кривой стока ведем в табличной форме (см. табл.№1.1).

Далее, строим интегральную кривую стока в прямоугольной системе координат (График №1).

Также был построен лучевой масштаб.

Для его построения необходимо

Масштаб стока m_w= 10⁸м³*см.

Масштаб времени m_t= 2,63*10⁶с*см.

Количество единиц расхода в 1 см чертежа m_Q= 10⁸м³*см.

P - полюсное расстояние.

1.2. ПОСТРОЕНИЕ ИНТЕГРАЛЬНОЙ КРИВОЙ СТОКА В КОСОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ ПО СРЕДНЕМЕСЯЧНЫМ РАСХОДАМ РЕКИ ДОЛГАЯ:

Следует отметить, что пользоваться кривой, построенной и прямоугольной системе координат, не совсем удобно, если имеется много лет наблюдений или значения стока велики. Кривая в этом случае растет вверх и в длину. Суммарная кривая имеет более компактный вид в косоугольной системе координат, особенно, если в качестве одной из осей использовать прямую, которой в прямоугольной системе координат соответствует средний многолетний расход.

Прямую, соответствующую среднему расходу, поворачиваем на угол a₀ но часовой стрелке. Эта прямая в новой системе координат станет горизонтальной и принимается осью времени t, а действительная ось времени займет положение t₀. При построении кривой стока в косоугольной системе координат мы увеличиваем масштаб стока (т.е. уменьшаем масштабный коэффициент), оставив масштаб времени без изменения.

Таким образом при построении кривой стока в косоугольной системе координат необходимо произвести вычисления:

ΔW_ik=W_i-_i

При вычислении величин ΔW необходимо учитывать знак, причем положительные значения откладываем над новой осью t, а отрицательные под нею.

Для того, чтобы определить сток в прямоугольной системе координат, например к моменту времени t_i, необходимо восстановить перпендикуляр в этой точке к оси t до пересечения с кривой стока и провести через точку пересечения прямую параллельную оси t₀. Точка пересечения этой прямой с осью W даст величину искомого стока.

Необходимость обращаться каждый раз к оси W, создает неудобства при пользовании такой системой координат. В связи с этим обычно выбирают на оси W величину стока W₀ кратную 2, 5, 10, проводят через точку W₀ прямую, параллельную оси t₀, определяют расстояние до точки пересечения этой прямой с осью t:

Рис. 3.

Рис. 4.

Откладывая на оси t последовательно отрезки 2х, 3х, 4х и т.д., проводим через соответствующие точки линии, параллельные оси t_o. Очевидно, что второй линии будет соответствовать сток 2W_o, третьей - 3W_o и т.д. При этом сама ось W становится ненужной. Сток легко определяется путем интерполяции, осуществляемой с точностью, с какой определяется сток при использовании оси W, так как расстояние по вертикали между двумя любыми соседними линиями равно W_o.

Как видно из рис.4

Y = W_o;

X = ;