Моделирование показателей надежности технических систем с использованием аппарата марковских случайных процессов

Задание для расчетно-графической работы «Моделирование показателей надежности технических систем с использованием аппарата марковских случайных процессов»

Вариант  1

Представим автомобиль как некоторую систему S с дискретными состояниями , которая переходит из состояния  в состояние под воздействием пуассоновских потоков событий (отказов) с интенсивностями . Будем рассматривать следующие состояния автомобиля, в которых он может находится в процессе эксплуатации и которые характеризуются целодневными  простоями:

- исправен, работает;     

- проходит техническое обслуживание;

- находится в текущем ремонте;

- находится в «капитальном ремонте;

- проводится замена агрегата;  

- исправен, не работает по организационным причинам;

- исправен, не работает, выходные и праздничные дни;

- списывается.

Рассматриваемые состояния  автомобиля характеризуются средним числом дней пребывания автомобиля в каждом j-м состоянии (j = 1, 2, ..., n)  . Отношение

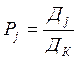
Где  — число календарных дней в году, можно трактовать как вероятность нахождения, автомобиля j-м состоянии .

Вероятности  являются функциями пробега автомобиля.

Вероятность нахождения автомобиля в состоянии  («исправен, работает»)  представляет собой коэффициент выпуска автомобиля — один из основных показателей работы автопредприятия.

Возможные переходы автомобиля из состояния  в состояние  описаны матрицей переходов.

Соответствующие интенсивности потоков событий , переводящих автомобиль из состояния  в состояние , определяются по формулам, привёденным в табл. П.11.1.

Таблица П.11.1

Интенсивности перехода

Требуется:

1. Построить размеченный граф состояний системы S – автомобиль по заданной матрице переходов.
2. Определить интенсивности , используя формулы табл. П.11.2.

Исходные данные для определения :

среднесуточный пробег — 0,2 тыс. км;

среднее время простоя автомобиля в текущем ремонте- 1,5 дня;

среднее время простоя по организационным причинам - 2 дня; остальные данные выбираются, исходя из профессиональных соображений.

3.   Составить систему дифференциальных уравнений Колмогорова и решить ее методом Рунге-Кутта с использованием стандартной программы на ЭВМ при следующих условиях:

а) пределы интегрирования: нижний -0, верхний -20; б) шаг интегрирования - 0,5;          .

в) начальные условия: ;

г) результаты вывести на печать в точках 1, 5, 10, 15, 20 с точностью .

4.   Получить значения коэффициента выпуска автомобиля  и построить график зависимости коэффициента выпуска от пробега.

5. Определить влияние на изменение коэффициенте выпуска среднесуточного пробега и среднего времени простоя в ремонте; изменение значения этих показателей на 40 - 60 %. Построить графики

Примечания

Интенсивность

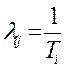
где  — среднее время пребывания в/-м состоянии.  

Интенсивность  для тыс. км.  

Для приведения всех интенсивностей перехода  к единым единицам измерения 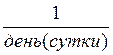 интенсивности перехода из 1-го состояния (автомобиль исправен) во все j-е состояния . При составлении дифференциальных уравнений умножаются на коэффициент (среднесуточный пробег).

Вариант 2

В процессе эксплуатации ЭВМ может рассматриваться как физическая система, которая в результате проверки может оказаться в одном из следующих состояний:

 - ЭВМ полностью исправна;

 - ЭВМ имеет незначительные неисправности в оперативной памяти, при которых она может решать задачи; 

 - ЭВМ имеет существенные неисправности и может решать ограниченный класс задач;

 - ЭВМ полностью вышла из строя;

  - ЭВМ находится на профилактике;

  - ЭВМ не работает по организационным причинам;

 - ЭВМ не работает, праздничные и другие нерабочие дни;

  ЭВМ списывается.     

Рассматриваемые состояния  ЭВМ характеризуются средним временем  пребывания ЭВМ и в каждом  j - м состоянии.

Отношение

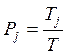
где Т — возможное время работы ЭВМ в данный период (месяц, квартал, год и т. д.), Можно трактовать как вероятность нахождения ЭВМ в j - м состоянии