Составление программы вычисления корней биквадратного уравнения. Построение графиков двух функций в одной области

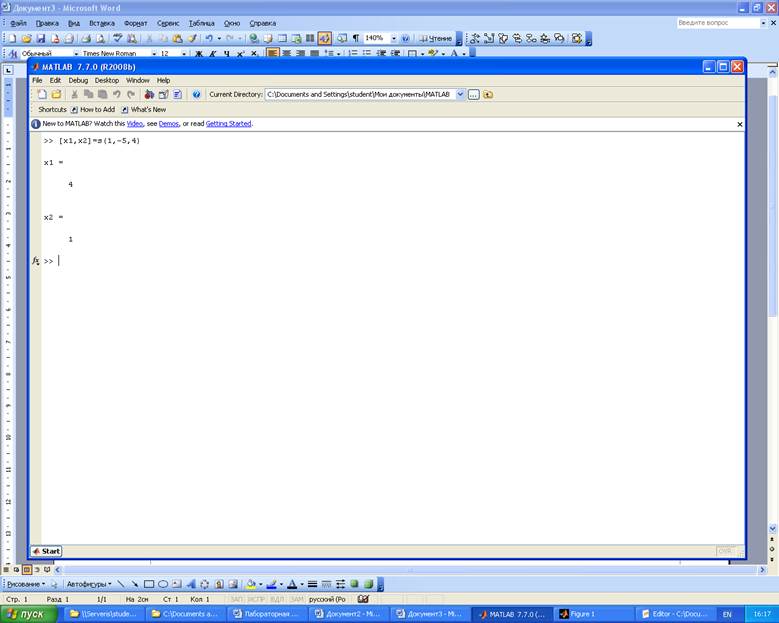
1. Составляем программу вычисления корней биквадратного уравнения   х² -5х +4 = 0. Получаем М-файл в виде function.

Листинг:

function [x1,x2]=s(a,b,c)

D=b^2-4*a*c;

x1=(-b+sqrt(D))/(2*a);

x2=(-b-sqrt(D))/(2*a);

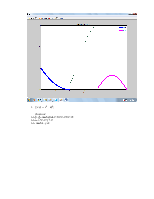
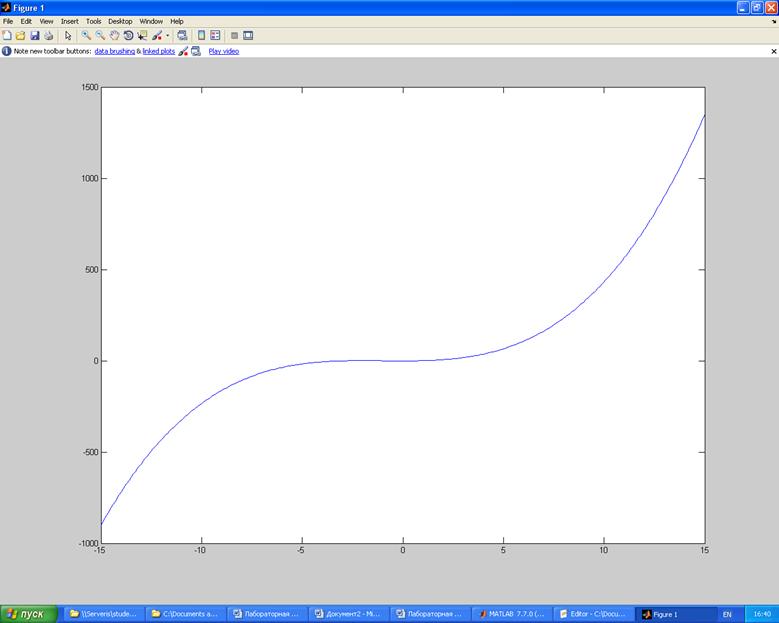
2. Построить графики функций:

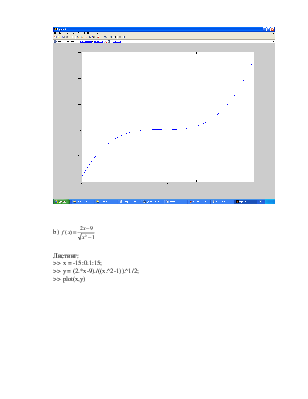
а)

Листинг:

>> x= -15:0.1:15;

>> y = ((1+x).*(x.^2+2.*x-2)).^1/3;

>> plot(x,y);

b)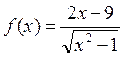

Листинг:

>> x = -15:0.1:15;

>> y = (2.*x-9)./((x.^2-1)).^1/2;

>> plot(x,y)

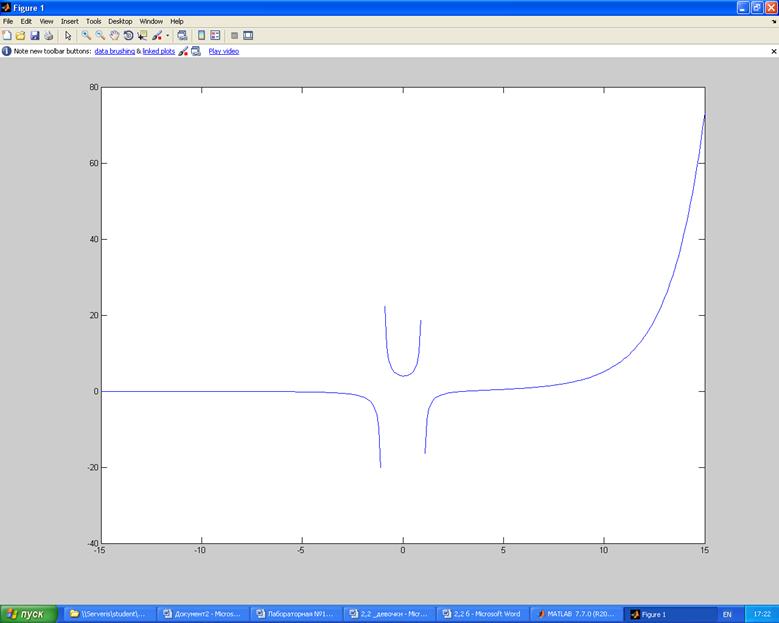
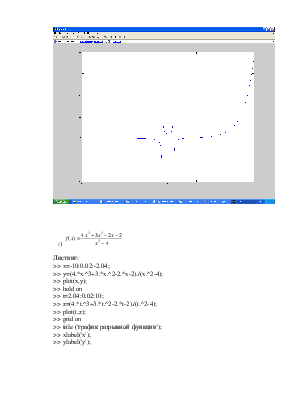
г)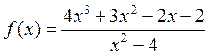

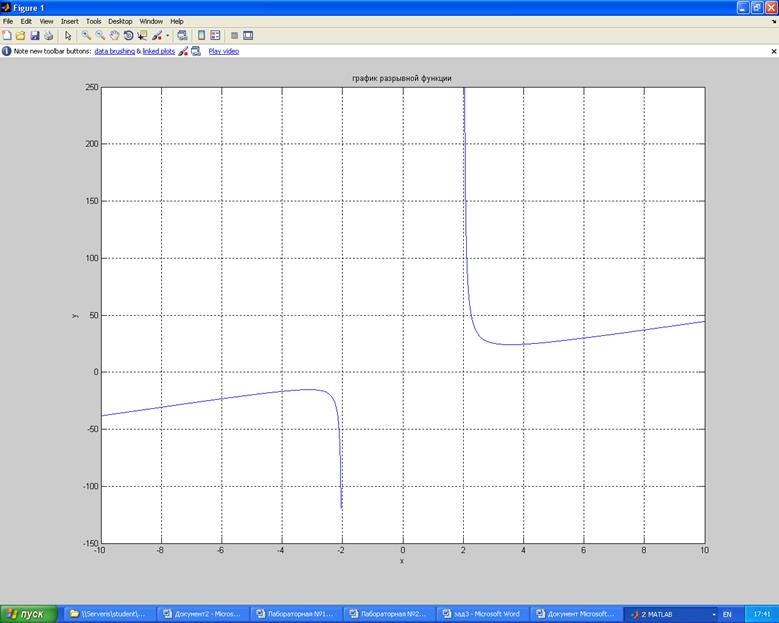
Листинг:

>> x=-10:0.02:-2.04;

>> y=(4.*x.^3+3.*x.^2-2.*x-2)./(x.^2-4);

>> plot(x,y);

>> hold on

>> t=2.04:0.02:10;

>> z=(4.*t.^3+3.*t.^2-2.*t-2)./(t.^2-4);

>> plot(t,z);

>> grid on

>> title ('график разрывной функции');

>> xlabel('x');

>> ylabel('y');

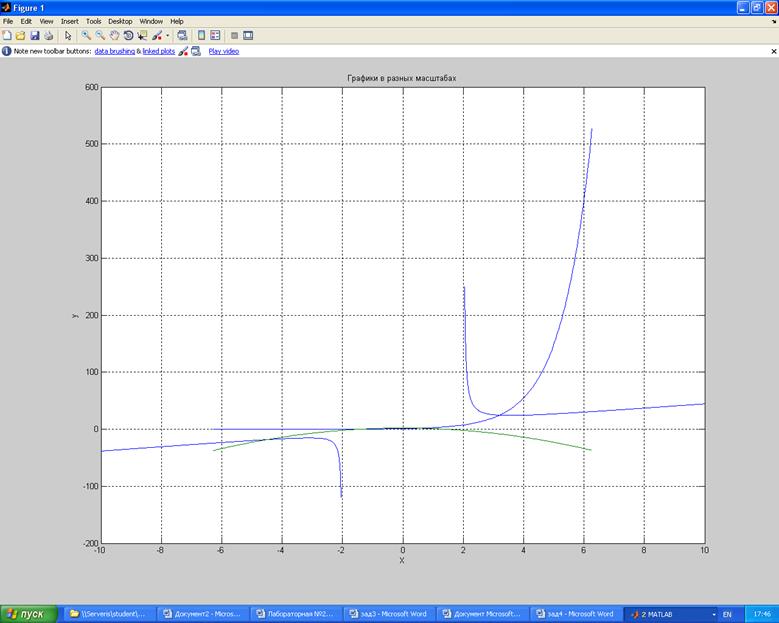
3. Построить графики двух функций в одной области:

Листинг:

>> x=-6.28:0.05:6.28;

>> y=exp(x);

>> z=2-x.^2;

>> plot(x,y,x,z);

>> grid on

>> title('Графики в разных масштабах');

>> xlabel('X');

>> xlabel('X');

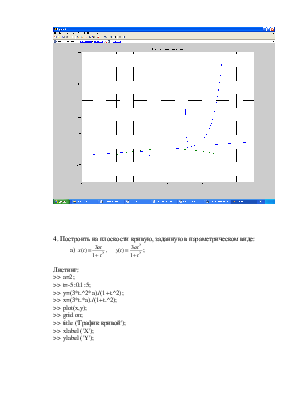
4. Построить на плоскости кривую, заданную в параметрическом виде:

a) ;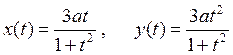

Листинг:

>> a=2;

>> t=-5:0.1:5;

>> y=(3*t.^2*a)./(1+t.^2);

>> x=(3*t.*a)./(1+t.^2);

>> plot(x,y);

>> grid on;

>> title ('График кривой');

>> xlabel ('X');

>> ylabel ('Y');

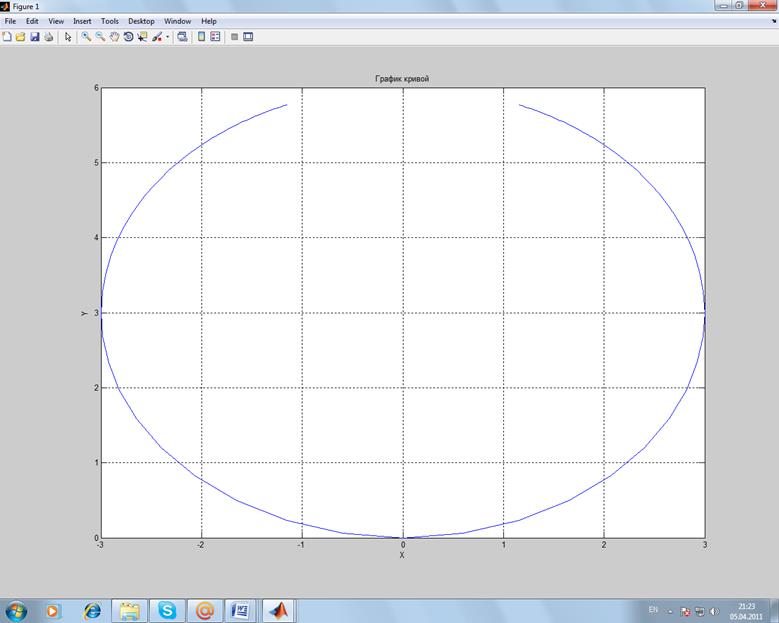
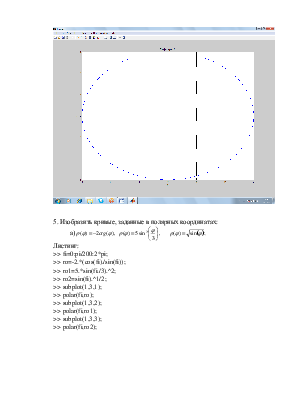
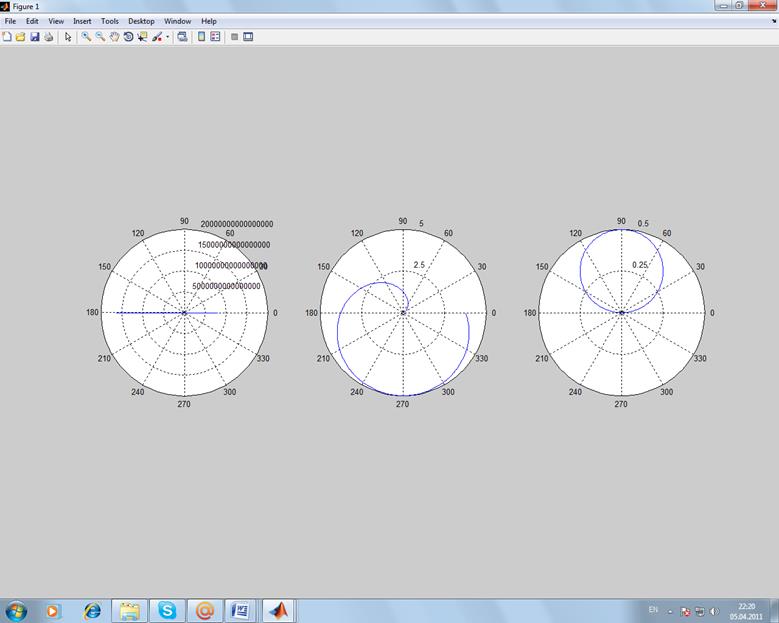
5. Изобразить кривые, заданные в полярных координатах:

а)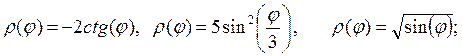

Листинг:

>> fi=0:pi/200:2*pi;

>> ro=-2.*(cos(fi)./sin(fi));

>> ro1=5.*sin(fi./3).^2;

>> ro2=sin(fi).^1/2;

>> subplot(1,3,1);

>> polar(fi,ro);

>> subplot(1,3,2);

>> polar(fi,ro1);

>> subplot(1,3,3);

>> polar(fi,ro2);

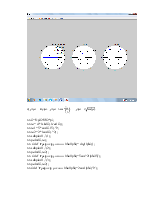
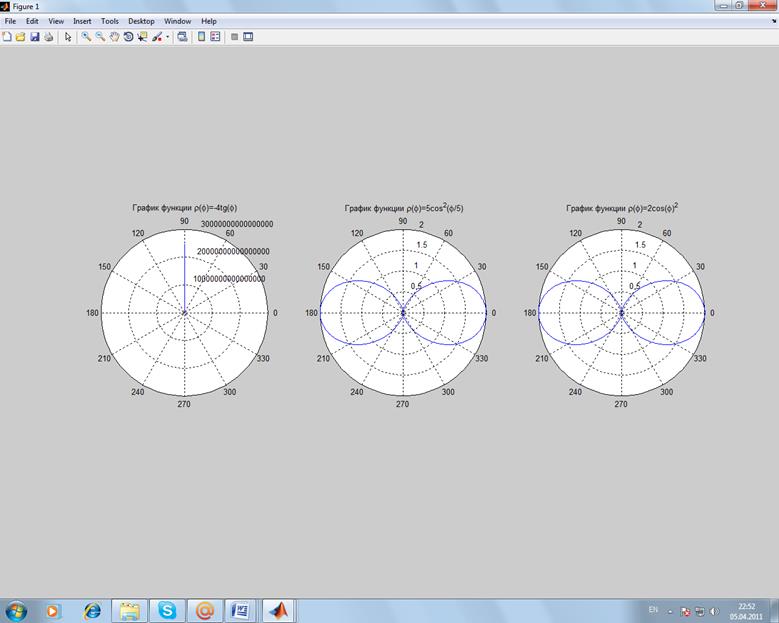
б)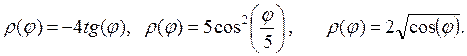

>> fi=0:pi/200:2*pi;

>> ro=-4.*(sin(fi)./cos(fi));

>> ro1=5.*cos(fi./5).^2;

>> ro2=2.*(cos(fi).^2);

>> subplot(1,3,1);

>> polar(fi,ro);

>>  title(' График функции \rho(\phi)=-4tg(\phi)');

>> subplot(1,3,2);

>> polar(fi,ro2);

>>  title(' График функции \rho(\phi)=5cos^2(\phi/5)');

>> subplot(1,3,3);

>> polar(fi,ro2);

>> title(' График функции \rho(\phi)=2cos(\phi)^2');

Форматирование двумерных графиков

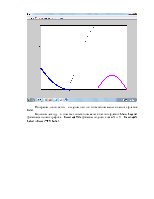
1.  Построить график заданной функции:

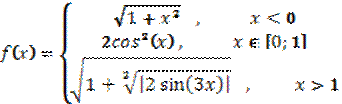
Сформируем массивы x, y, t,z,a и b и построим график функции у(х) с помощью функции plot.

Листинг:

>> x=-1:0.01:0;

>> y=(1+(x.^2)).^1/2;

>>  t=0:0.01:1;

>> z=2.*cos(x).^2;

>> a=1:0.01:2;

>> b=(1+((abs(2.*sin(3.*x))).^1/3)).^1/2;

>> plot(x,y);

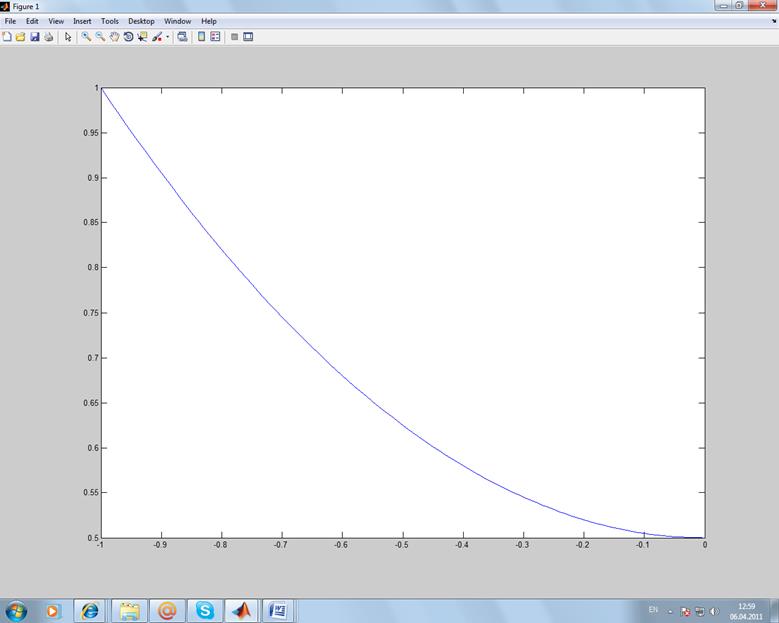
Добавляем график функции z(t) и b(a) в графическом окне. Для этого выделяем оси и в контекстном меню выбраем команду AddData.

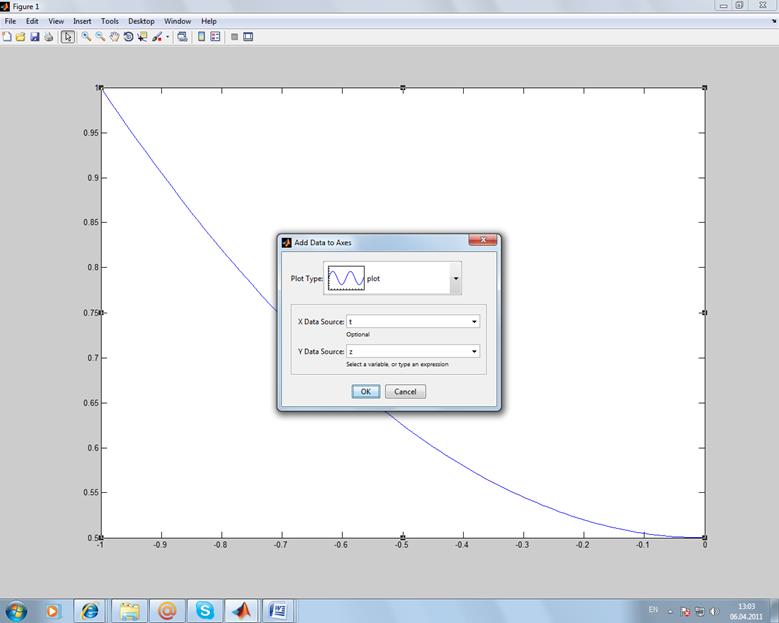
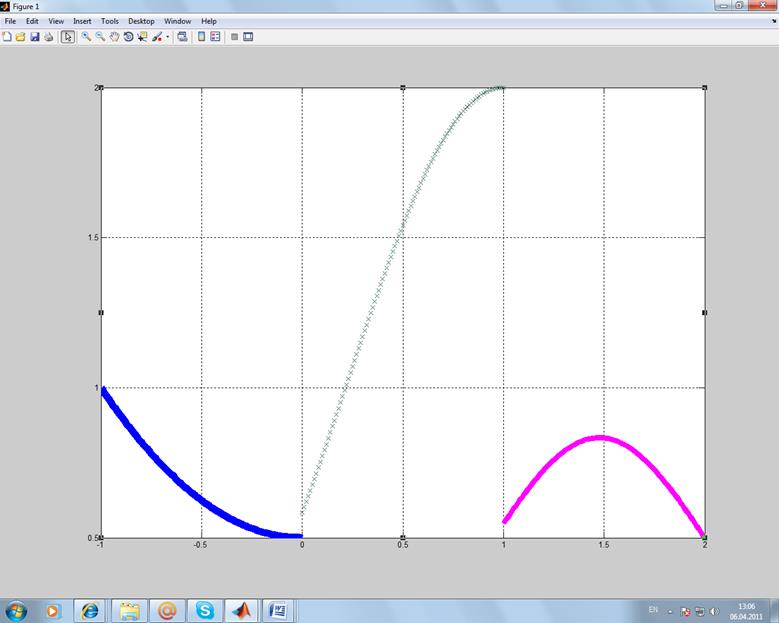
Изобразим линии сетки – выделим оси и в контекстном меню включить флажок Grid.

Включим легенду – в этом же контекстном меню включить флажок Show Legend. Добавим заголовок графика – Insert ® Title.Добавим подписи к осям Х и У – Insert ® X Label  и Insert ® Y Label.

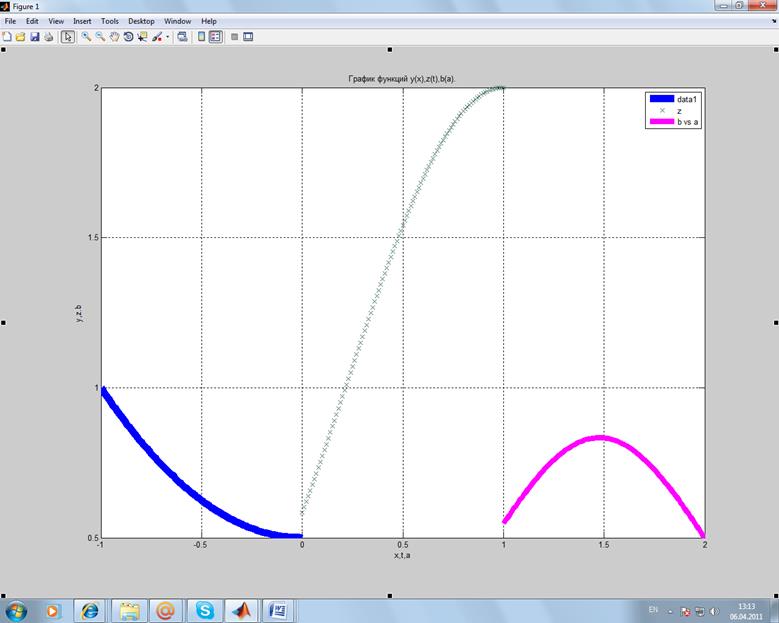
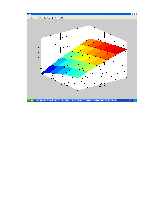
1.  z(x,y) = x² – 2y²;

Листинг:

>> [x y]=meshgrid(-2:0.2:2,-2:0.2:2);

>> z=x.^2-2.*y.^2;

>>  mesh(x,y,z);

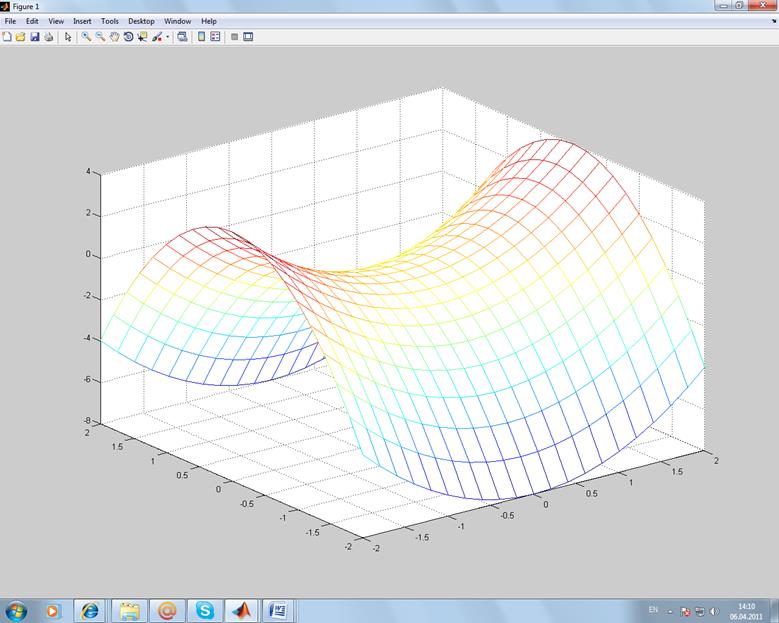
z(x,y)=3x² – 2 sin²(y) y²;

Листинг:

>> [x,y]=meshgrid (-2:0.2:2,-2:0.2:2);

>> z=3.*x.^2-2.*sin(x).*y.^2;

>> mesh(x,y,z);

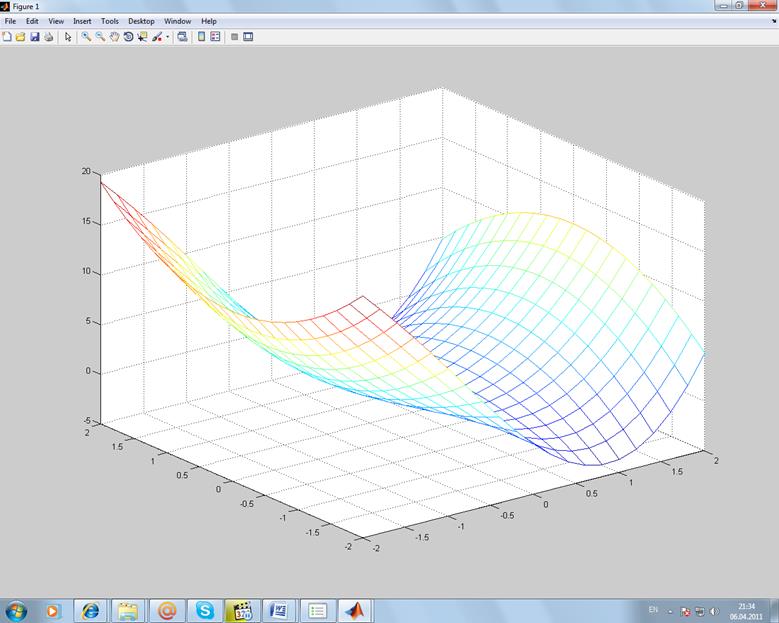
z(x,y)=3e^2x x – 2 y;

Листинг:

>> [x,y]=meshgrid (-2:0.2:2,-2:0.2:2);

>> z=(3.*exp(2.*x).*x)-2.*y;

>> mesh(x,y,z);

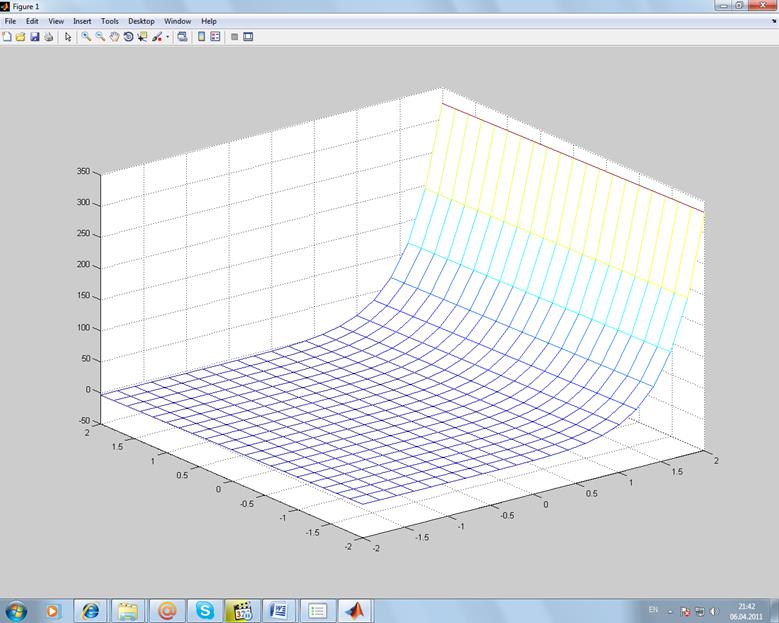
Листинг:

>> [x y]=meshgrid(-2:0.2:2,-2:0.2:2);

>> z=(sin(x)./y).*cos(y./x);

>> surf(x,y,z);

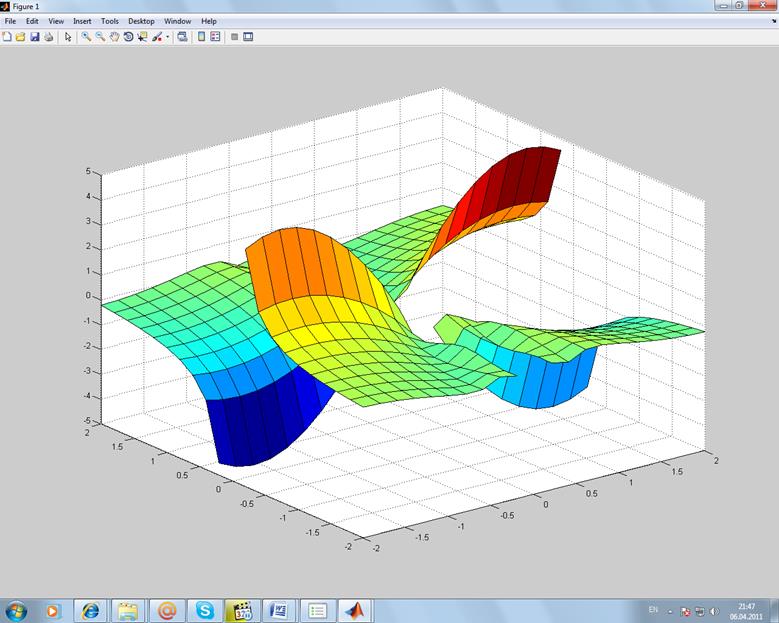
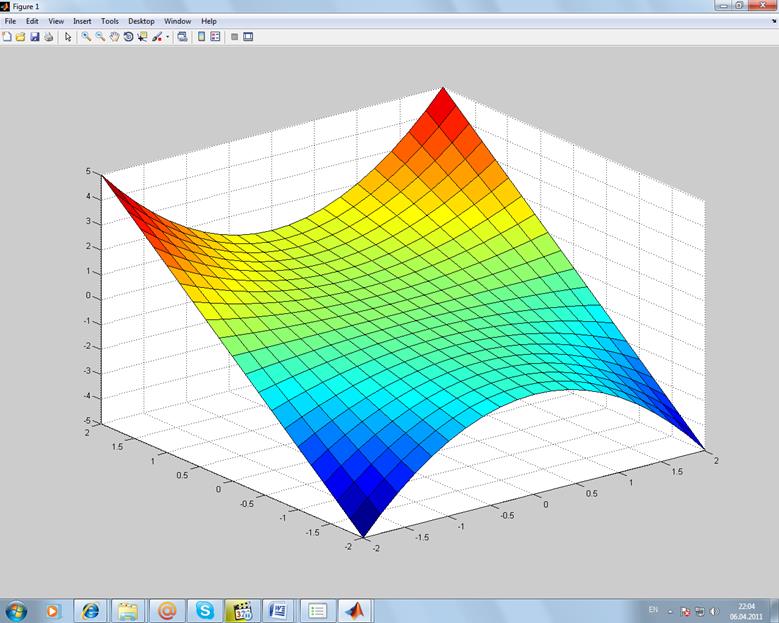
Листинг:

>> [x,y]=meshgrid(-2:0.2:2,-2:0.2:2);

>> z=y.^1/2.*(x.^2+1);

>> surf(x,y,z);

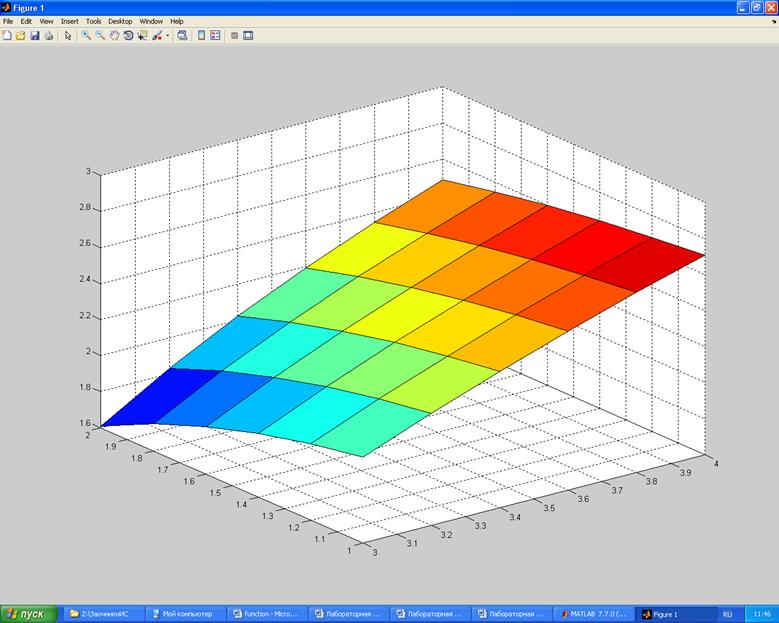
>> [x y]=meshgrid(3:0.2:4,1:0.2:2);

z=log(x.^2-y.^2);

surf(x,y,z);