Метод наименьших квадратов. Аппроксимирующая функция, страница 2

В случае показательной зависимости  ее можно свести к линейной путем логарифмирования: .

 Степенная зависимость  также сводится логарифмированием к линейной зависимости: .

Решение:

Так как заданная табличная функция y принимает отрицательные значения, то вычислить соответствующие логарифмы невозможно. Поэтому для аппроксимации следует выбрать функцию  и определить ее коэффициенты.

Пусть V = ln y, B = ln b,

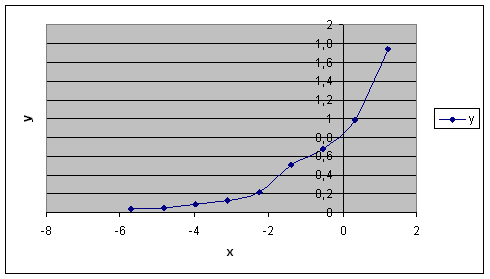
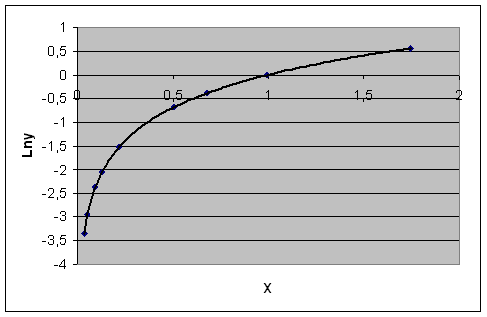
Рис. 1. Заданная табличная функция

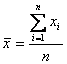= -2,247,

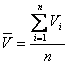= -1,415,

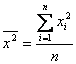= 10,032,

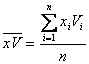= 6,04.

            Подставив эти значения в систему (1) определим коэффициенты a и b:

,          

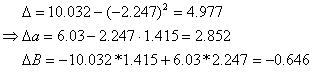
,           ;b=0.88

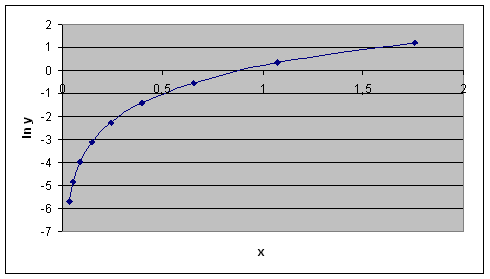
Рис. 2 Заданная  аппроксимирующая функция