Магнитное поле. Зависимость магнитного поля от расстояния

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

Кафедра общей и технической физики

Лабораторная работа №13

Изучение магнитного поля тока

Выполнил студент группы:  ПГ-99  Коновалов С.Ю.

                                 Проверил:  доцент Корольков А.П.

Санкт-Петербург

2000

Цель работы:

            Изучить магнитное поле, создаваемое током, текущим по прямоугольной рамке. Измерить с помощью индукционного датчика, соединенного с ламповым вольтметром, магнитное поле нижнего участка этой рамки при различных расстояниях до него. Построить график зависимости магнитного поля от расстояния и сравнить его с теоретическим, полученном на основании закона Био- Савара- Лапласа.

Общие сведения:

            Вокруг проводника, по которому протекает электрический ток, существует магнитное поле, каждая точка которого характеризуется вектором напряженности (рис.1). Вектор  может быть найден как сумма векторов напряженности , создаваемых каждым малым участком проводника с током:

            Согласно закону Био- Савара- Лапласа

,

где I- сила тока в проводнике; - вектор, имеющий длину отрезка  и направленный вдоль тока; - радиус- вектор, проведенный из элемента  в рассматриваемую точку Р.

Вектор  направлен перпендикулярно плоскости, проведенной через  и , и связан с направлением тока правилом правого винта:

.

            Для прямолинейного проводника с током конечной длины (рис.2) все , создаваемые отдельными элементарными участками в точке поля Р, направлены в одну сторону ( перпендикулярно плоскости чертежа). В этом случае напряженность магнитного поля в точке Р может быть найдена интегрированием:

.

            Произведем вычисления в СИ, найдем, что

                                                           ,                      (1)

где - кратчайшее расстояние от точки Р до проводника с током; - углы между крайними элементами проводника  и соответствующими радиус- векторами РА и РВ.

                        Рис.1                                                                         Рис.2

            Если определить напряженность в точках, расположенных на перпендикуляре, восстановленном в середине проводника, то

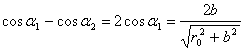                                 (2)

            С учетом выражения (2) формулу (1) можно записать в виде