


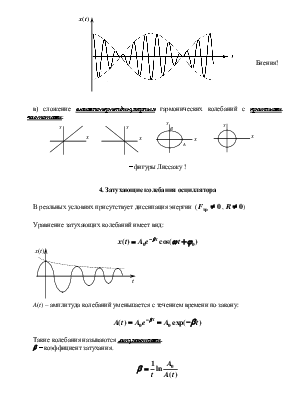
















Электромагнитные волны, распространяясь в пространстве, могут накладываться друг на друга. Результат наложения можно рассчитать по принципу суперпозиции: результирующее колебание в каждой точке представляет собой геометрическую сумму колебаний, соответствующих каждой из складываемых волн. Амплитуда результирующего колебания очень сильно зависит от разности фаз складываемых волн:
Волны, у которых разность фаз не зависит от времени (Dj = const) называются когерентными волнами (для этого необходимо, чтобы волны были монохроматичными (с одинаковой частотой) и разность начальных фаз у них была постоянной Dj0 = const).
Явление наложения двух или нескольких когерентных волн друг на друга, при котором наблюдается устойчивая картина усиления (max) или ослабления (min) амплитуды результирующей волны, а, следовательно, и перераспределение энергии и интенсивности волн, называется интерференцией.
Волны, у которых Dj¹const, называются некогерентными, в результате их сложения интерференционной картины не наблюдается, результирующая амплитуда во всех точках в среднем одинаковая.
Результат интерференции когерентных волн очень сильно зависит от оптической разности хода лучей:
![]() ,
(2)
,
(2)
где s = nℓ - оптическая длина пути луча (ℓ - геометрическая длина пути луча). В точках, для которых выполняется условие
![]() где m = 0, 1, 2, …,
(3)
где m = 0, 1, 2, …,
(3)
наблюдаются интерференционные максимумы. Следовательно, условие (3) является условием максимума интерференции.
В точках, для которых выполняется условие
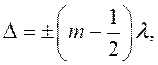 где m = 1, 2, 3, …,
(4)
где m = 1, 2, 3, …,
(4)
наблюдаются интерференционные минимумы. Следовательно, условие (4) является условием минимума интерференции.
Целое число m в формулах (3), (4) называется, соответственно, порядком максимума или минимума интерференции.
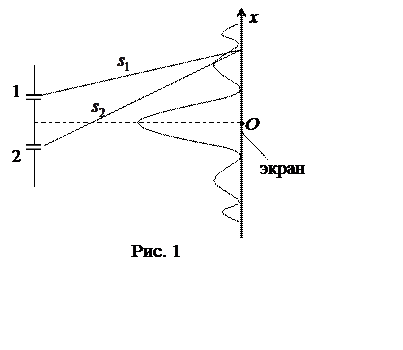 Естественные
источники света излучают некогерентные волны, т. к. возбужденные атомы излучают
спонтанно и
Естественные
источники света излучают некогерентные волны, т. к. возбужденные атомы излучают
спонтанно и ![]() Поэтому долгое
время не удавалось наблюдать интерференцию видимых лучей. Первым наблюдал
интерференцию световых волн английский физик Юнг. Он догадался разделить свет
от одного источника на части с помощью непрозрачной ширмы с параллельными щелями.
В итоге лучи, идущие от щелей, становились когерентными, и на экране наблюдалась
типичная интерференционная картина (рис. 1).
Поэтому долгое
время не удавалось наблюдать интерференцию видимых лучей. Первым наблюдал
интерференцию световых волн английский физик Юнг. Он догадался разделить свет
от одного источника на части с помощью непрозрачной ширмы с параллельными щелями.
В итоге лучи, идущие от щелей, становились когерентными, и на экране наблюдалась
типичная интерференционная картина (рис. 1).
Положение максимумов и минимумов на экране можно найти по формулам:
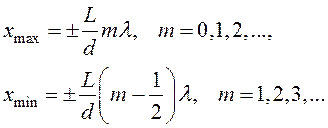 (5)
(5)
где L – кратчайшее расстояние от щелей 1, 2 до экрана;
d – расстояние между щелями 1 и 2.
В реальном опыте Юнга волны, распространяющиеся от щелей, не являются плоскими – их амплитуда убывает с увеличением расстояния от щелей, поэтому интенсивность максимумов на экране убывает с ростом порядка m (см. рис. 1).
Из естественных проявлений интерференции света наиболее известно радужное окрашивание тонких пленок, возникающее в результате интерференции света, отраженного от верхней и нижней поверхностей пленки. Наиболее простой для рассмотрения случай, когда параллельный пучок света падает под углом a на тонкую пленку постоянной толщины d.
Возникающая при этом оптическая разность хода отраженных (1 и 2) или проходящих (1¢ и 2¢) лучей (рис. 2) вычисляется по формуле:
![]() (6)
(6)
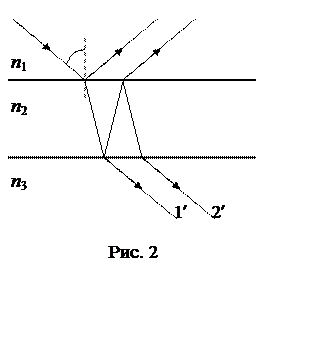 где D0 - дополнительная разность хода, возникающая из-за отражения луча от
оптически более плотной среды.
где D0 - дополнительная разность хода, возникающая из-за отражения луча от
оптически более плотной среды.
Правило: при отражении луча света от оптически
более плотной среды фаза этого луча меняется на 180° и к оптической длине пути этого луча s нужно добавить ![]() При
отражении от менее плотной среды и при преломлении потери фазы не происходит.
При
отражении от менее плотной среды и при преломлении потери фазы не происходит.
Далее расчет результатов интерференции проводят с учетом условий максимумов (3) и минимумов (4) интерференции.
Если на тонкую пленку постоянной толщины падает свет под разными углами, то на пленке наблюдаются интерференционные полосы в точках, куда свет
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.