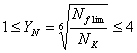Конструирование деталей передачи, валов, подшипниковых узлов, шпоночных соединений цилиндрической зубчатой передачи, страница 3

,

где  - базовое число циклов напряжений, . Вычислим значения  для шестерни и колеса соответственно:

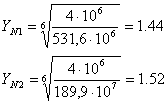
После вычислений коэффициентов долговечности, вычисляем допускаемое напряжение изгиба:

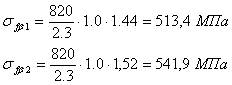
Для расчётов примем меньшее значение напряжения на изгиб, т.е. .

            Зная теперь все необходимые коэффициенты и величины, можем найти межосевое расстояние :

.

По стандартному ряду межосевых расстояний выбираем большее значение, чем 203,82, следовательно, примем .

            Определим ориентировочную оценку величины нормального модуля использования  и :

.

По стандартному ряду значений модуля для цилиндрических зубчатых колёс выбираем значение модуля, равным ..

Вычислим суммарное значение числа зубьев шестерни и колеса вместе и по отдельности. Для этого воспользуемся следующими формулами:

1.  Суммарное значение:

       Примем Z_c=98.

2.  Для шестерни и колеса отдельно:

     .

Примем для шестерни число зубьев равное 24, тогда число зубьев для колеса определим из выражения:  зубьев.

            Для продолжения расчётов необходимо уточнить межосевое расстояние и передаточное число, воспользовавшись формулами, принимая для косозубой передачи :

Исходя из полученных величин, необходимо рассчитать погрешность передаточного числа, которая не должна превышать 4%:

,

следовательно, такое передаточное число допустимо.

Определяем основные размеры шестерни и колеса по отдельности:

1. Шестерня:

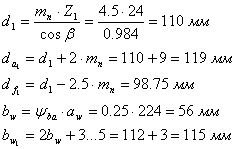
3…5 мм добавляем, т.к. эта величина является шириной канавки для выхода фрезы

2. Колесо:

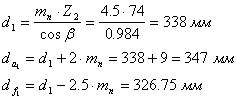
 - ширина зубьев венца

Определяем усилия в зацеплениях:

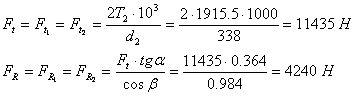
В выражении для радиальной силы , т.к. у передач, выполненных без смещения, угол зацепления равен .

           

            Выполним проверочный расчёт передачи на контактную прочность рабочих поверхностей зубьев.

1. Определим нормальное расчётное контактное напряжение:

,

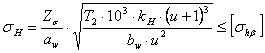где ,  - коэффициент нагрузки, . Зная все параметры, находим расчётное напряжение:

,