Колебательное движение материальной точки

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт

(Технический Университет)

Кафедра механики

Расчётно-графическая работа № 1

Дисциплина: Теоретическая механика.

Тема: Колебательное движение материальной точки.

Вариант № 3.

Выполнил: студент группы ТПП-00-2       _____________       / Дейчман Д.А/

Проверил: доцент кафедры механики    _____________      / Монахов В.Н./                     

Санкт-Петербург

2002 г.

Исходные данные:                   Задание: груз массой mприкреплён к пружине                      жёсткостью c. Начальная деформация пружины _0,

начальная скорость груза V₀.

С = 10 Н/см =1000 Н/м                                 Найти: уравнение движения груза, амплитуду, час-

l₀ = 0 см                                                          тоту и период колебаний, наибольшее значение мо-

m = 28Ö2 кг                                                     дуля силы упругости.

V₀ = = 0 см/с

a = 45°

Расчетная схема:

 

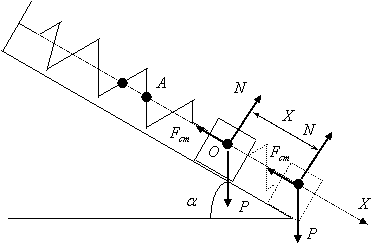                                                 М_о

Рассмотрим условие статического равновесия груза:

å X = P sina - F_ст = 0

             P sina - cl_ст = 0

l_ст = P sina / с = mg sin 45° / c = 28Ö2*10*0.7 / 1000 = 0.3 м = 30 см .

Рассмотрим движение груза (положение М):

На основании закона Гука:

F = c*l = c*(l_ст + x)

c*l_ст = P sina                                                                                    (1)

F = c*l_ст + c*x = c*x + P sin 45°                                                      (2)

Составляем дифференциальное уравнение движения груза:

mx = X , где X – проекция сил  на ось Ox

X = P sina - F = P sin 45° - cx - P sin 45° = - cx

mx = - cx – дифференциальное уравнение движения груза.

с / m = k² , где k – частота

k = Öc / m  = Ö1000 / 392 = 2.6 c^-1

x + k²*x = 0 – линейное дифференциальное уравнение второго порядка.

Решением этого уравнения является зависимость

x = C₁*cos k*t + C₂*sin k*t                                                              (3)

где C₁ , C₂ – постоянные коэффициенты, зависящие от начальных условий.

В начальный момент груз находится в точке О

l₀ = 0

x₀ = - OM = -l₀ - l_ст = -30 см.

Начальная скорость  V₀ = x₀ = 0

x = - C₁*k*sin k*t + C₂*k*cos K*t                                                    (4)

Подставляем в уравнения (3) и (4) значения начальных условий:

t = 0

(3)  x₀ = C₁*cos k*0 + C₂*sin k*0 = C₁*1 + C₂*0

C₁ = x₀ = - 30 см

(4)  x₀ = - C₁*k*sin k*0 + C₂*k*cos K*0 = - С₁*k*0 + C₂*k*1

C₂ = x₀ / k = 0 / 2.6 = 0