Матрицы рассеяния. Основные положения применения матриц рассеяния в СВЧ технике, страница 2

при этом 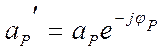 , а фазы отраженной волны к увеличению на величину , при этом .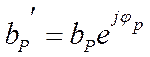

Здесь  и - комплексные амплитуды падающей и отраженной волн в новой плоскости отсчета.

При перемещении плоскостей отсчета во всех плечах многополюсника должна быть записана новая матрица рассеяния

, причем произвольный элемент матрицы

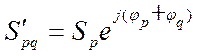
Значения  и положительные при сдвиге плоскостей отсчета в сторону соединения и отрицательные при сдвиге в сторону удаления от рассматриваемого многополюсника.

Рассмотрим, каким образом можно определить элементы векторов

 и , если плоскость отсчета не совпадает с плоскостью размещения нагрузки на примере плеча р.

Возможны два варианта.

Вариант первый.

Плоскость отсчета переносится в сторону соединения (рис.    (а))

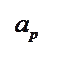
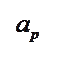
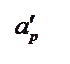
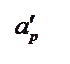
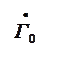
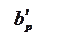
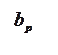
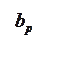
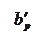
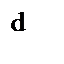
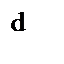
а)                                                               б)

Рис. Преобразование нагрузки.

а) – изменение плоскости отсчета, б) – изменение положения нагрузки.

Так как коэффициент отражения от нагрузки 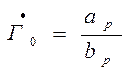 , то при перемещении в сторону соединения фаза уменьшится на величину 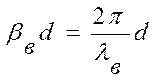, а фаза увеличится на величину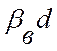

поэтому в новой плоскости отсчета

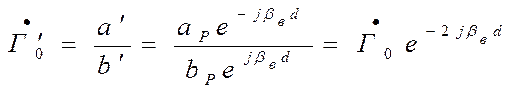
Вариант второй.

Плоскость отсчета остается постоянной, а нагрузка переносится в плоскость р`

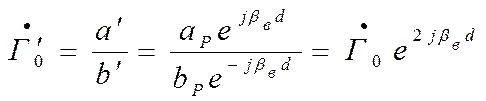
В этом случае фаза   увеличивается на величину 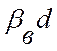, а фаза  уменьшается на величину  .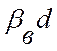

В частном случае, наиболее часто применяемом в измерениях, в качестве нагрузки применяется короткозамыкающий поршень, перемещаемый вдоль линии передачи.

При этом 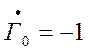 и

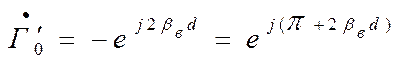
значение - положительное при передвижении короткозамыкающего поршня к соединению и отрицательное – при его перемещении от многополюсника.

Измерение элементов матрицы рассеяния.

Возьмем четырехполюсник. Для него

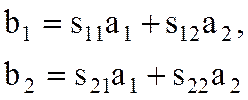
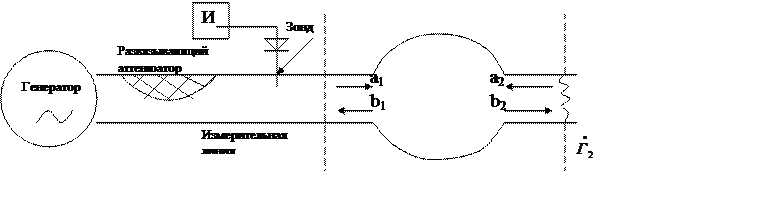
Рассмотрим схему измерений (рис.   )

 

Рис. Схема для определения элементов матрицы рассеяния.

Значение 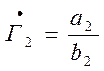. Подставим это значение в записанные ранее выражения для b₁ и b₂ и получим

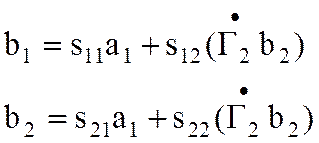
Найдем из последних соотношений значение 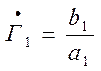 . Из второго выражения получаем .

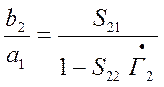Подставляя значение b₂  из последнего выражения в первое, получим

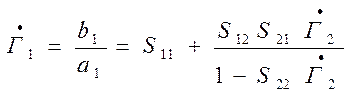
На основании последнего выражения можно разработать различные методы определения элементов матрицы рассеяния.

Включая в плечо 2 согласованную нагрузку (а₂ = 0, 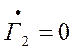), получим 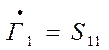, то есть S₁₁ – представляет собой коэффициент отражения от входа 1-1 четырехполюсника при согласованной нагрузке на входе 2-2.

Аналогично, S₂₂ – коэффициент отражения от входа 2-2 при согласованной нагрузке на входе 1-1.

При а₂ = 0 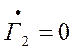 () имеем  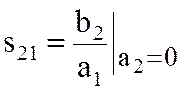отсюда S₂₁ – коэффициент передачи со входа 1 на вход 2 при условии согласования входа 2.

И последний элемент 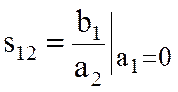  есть коэффициент передачи со входа 2 на вход 1 при согласовании входа 1.

Вывод.     Измеряя коэффициенты отражения и передачи при условии согласования плеча четырехполюсника, к которому не подключен генератор, можно определить все значения элементов матрицы рассеяния четырехполюсника.

В случае взаимного четырехполюсника, когда S₁₂ = S₂₁  можно определить значения элементов матрицы рассеяния методом короткого замыкания (рис.   )

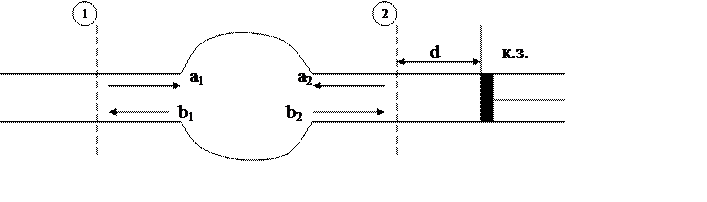
Рис.   Метод короткого замыкания.

При расположении к.з. поршня в плоскости 2 () производится измерение коэффициента отражения в плоскости 1 (на входе четырехполюсника), при этом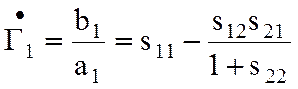

Затем к.з. поршень перемещается на расстояние 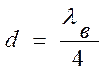, т.е. в плоскость 2 () и снова производится измерение коэффициента отражения в плоскости 1, при этом

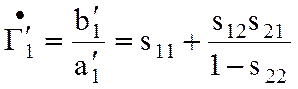
В плечо 2-2 ставится согласованная нагрузка и определяется

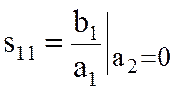затем вычисляется S₂₂ из выражения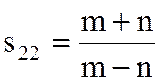

где 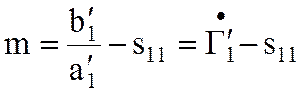          и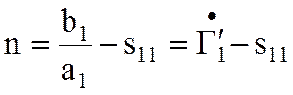         

Далее определяется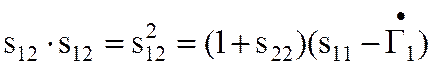 

Возможны и другие методы определения элементов матрицы рассеяния по произведенным измерениям.

При рассмотрении многополюсников рассматриваются поочередно по два входа при работе остальных  на согласованные нагрузки и определяются параметры выделенных четырехполюсников.

Например, имеем систему уравнений, связывающую входные волны с отраженными через коэффициенты матрицы рассеяния.

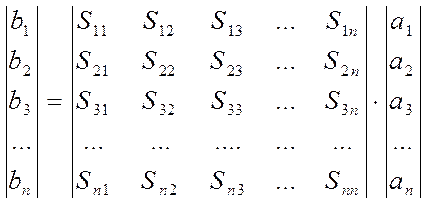
При условии согласовании всех плеч, кроме первого а₁ ¹ 0; а₂ = а₃, ..а_n = 0. Имеем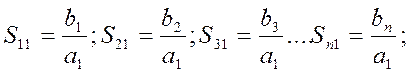

S₁₁ -  коэффициент отражения от первого входа.

S₂₁, S₃₁, .. S_n1 – коэффициенты передачи с первого входа на второй, третий, … n – ый входы.

При условии согласовании всех плеч, кроме второго а₂ ¹ 0; а₁ = а₃ = а₄…= а_n = 0 

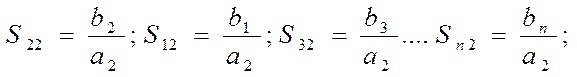
Здесь S₂₂  - коэффициент отражения от второго входа.

S₁₂, S₃₂, S₄₂… S_n2 – коэффициент передачи со второго на первый, третий, …. n – ый входы.