Комплексное значение суммарной поперечной электрической составляющей равна
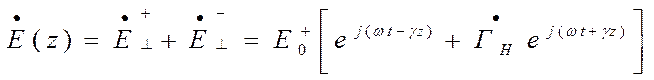
Аналогично для суммарной поперечной магнитной составляющей
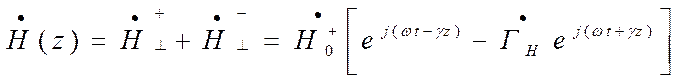 , где
, где ![]() - коэффициент отражения от
нагрузки
- коэффициент отражения от
нагрузки
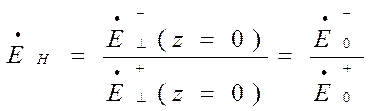
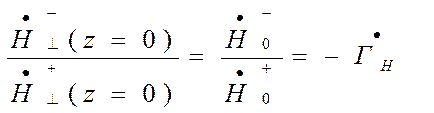 .
.
Вынесем за скобки множитель 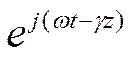 и
получим
и
получим
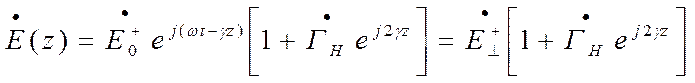 ( )
( )
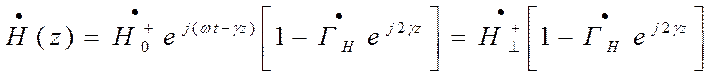 ( )
( )
По определению коэффициент отражения в плоскости z.
 ( )
( )
С учетом ( ) уравнения ( ) и ( ) можно записать в виде
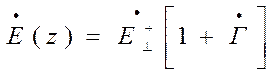 ,
,
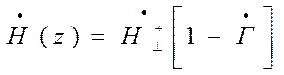 ( ),
( ),
Из выражений ( ) видно, что амплитуда суммарной
электрической составляющей, как и суммарной магнитной составляющей поля,
зависит от координаты z. Она достигает максимального
значения, равного 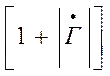
и минимального 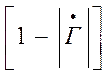 .
.
Отношение максимального значения к минимальному называется коэффициентом стоячей волны по напряжению.
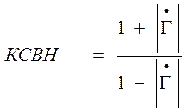 или
или 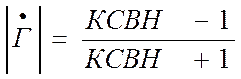
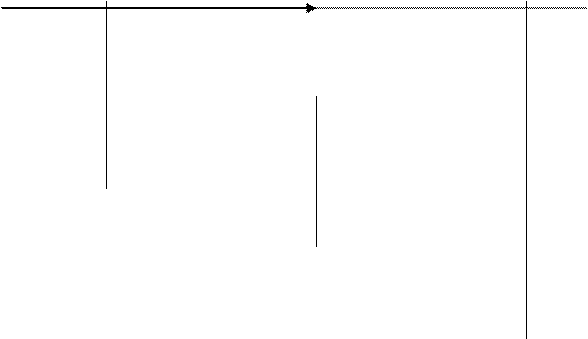
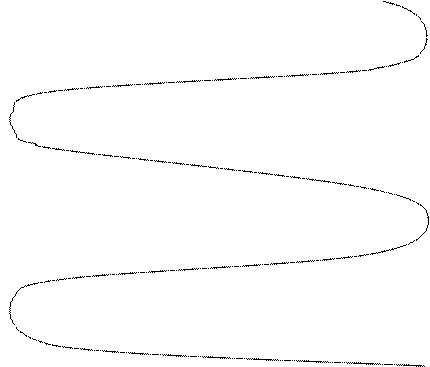
С помощью построения зависимости 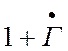 на
комплексной плоскости можно показать процесс образования интерференционной
картины сложения прямой и отраженной волн в линии передачи (см. рис. 2).
на
комплексной плоскости можно показать процесс образования интерференционной
картины сложения прямой и отраженной волн в линии передачи (см. рис. 2).
Входное сопротивление. Под входным сопротивлением в
произвольном сечении z линии передачи понимают
отношение 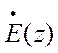 к
к 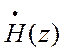 в
рассматриваемом сечении линии.
в
рассматриваемом сечении линии.
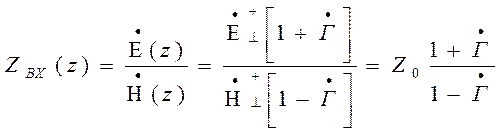 ( )
( )
Наиболее часто применяется нормированное значение входного сопротивления.
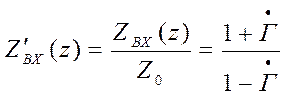 , ( )
, ( )
или
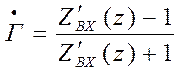
![]()
. ( )
При значении z = 0 имеем
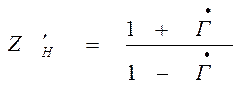 ,
( )
,
( )
или
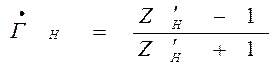
Последние выражения устанавливают связь между коэффициентом отражения, фаза и амплитуда которого может быть измерена на сверхвысоких частотах и сопротивлением, величина и характер которого определяется при измерениях напряжения и тока на низких частотах (в электрических цепях).
![]() +j
+j
к нагрузке
 |
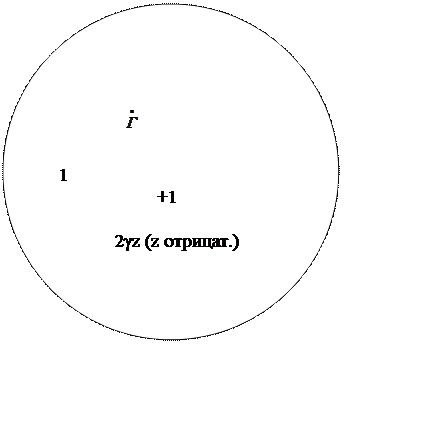 Z = 0
Z = 0
 |
|||
![]()
![]()
![]()
![]() к генера-
к генера-
![]()
![]() тору
тору
 |
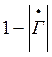
![]()
![]()
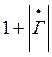
![]()
![]() +1
+1
![]()
![]()
![]()
![]() 0
0
К генера- lВ/2
![]() тору
тору
![]()
![]()
![]()
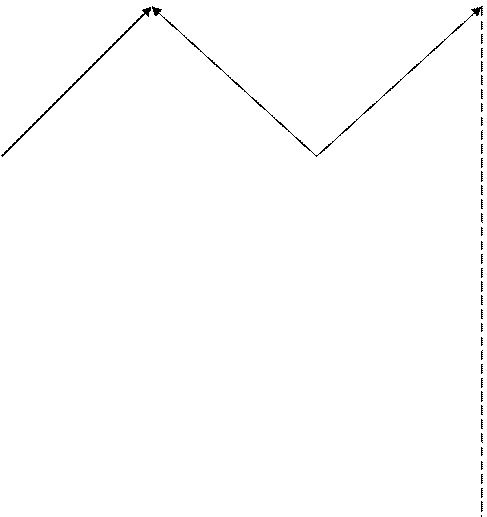
Рис.2 Образование интерференционной картины поля.
Значение передаваемой мощности можно выразить через значения ![]() и
и ![]() и
коэффициент отражения
и
коэффициент отражения ![]() .
.
Так как ![]() и
и ![]() находятся
в фазе, а
находятся
в фазе, а ![]() не зависит от поперечных координат
не зависит от поперечных координат
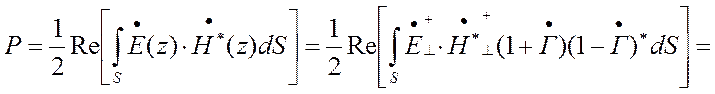
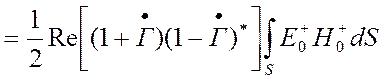
Так как 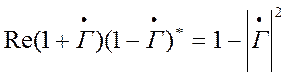 , то
, то
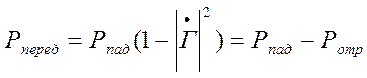 (
)
(
)
В случае бегущей волны в волноводе 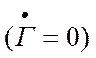 передаваемая
мощность была выражена через
передаваемая
мощность была выражена через ![]() и Z0 или
и Z0 или ![]() и Z
0.
и Z
0.
Аналогично при наличии отраженной волны
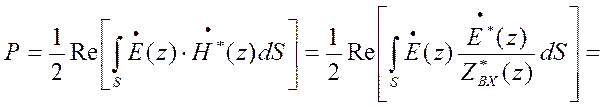
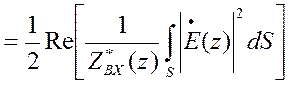 , так как
, так как 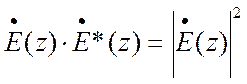
Входное сопротивление в любом сечении z можно выразить через Zн
Если известно сопротивление нагрузки 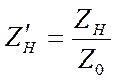 , то
коэффициент отражения от нагрузки
, то
коэффициент отражения от нагрузки 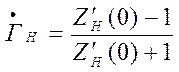
В произвольном сечении z коэффициент отражения равен
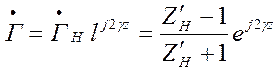 ( )
( )
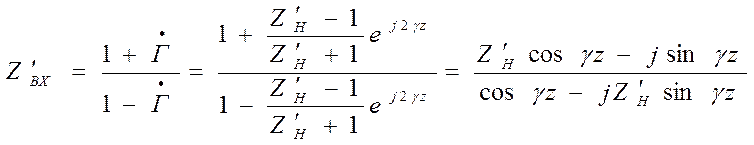 В случае отсчета направления от нагрузки к
генератору ( l = - z)
В случае отсчета направления от нагрузки к
генератору ( l = - z)
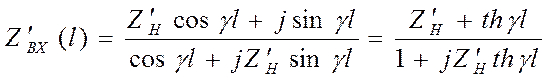 , ( )
, ( )
где g = b - ja.
При a = 0 последнее выражение принимает вид
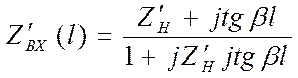 ,
( )
,
( )
аналогично для входной проводимости
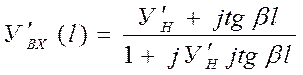 ( )
( )
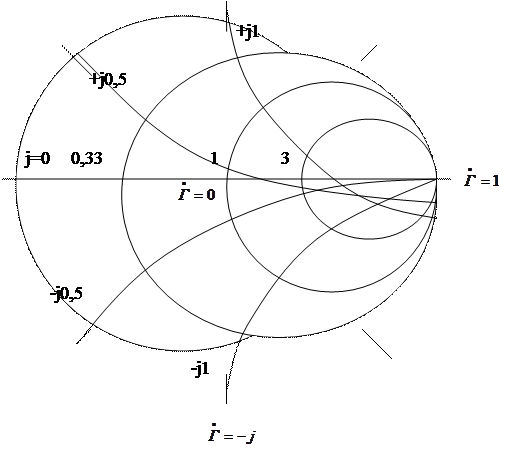
Расчеты с использованием аналитических выражений могут быть заменены использованием круговой диаграммы, показанной на рис. 3. Круговая диаграмма представляет собой круг, выделенный на комплексной плоскости, каждая точка которого соответствует одному из возможных значений коэффициента отражения, а так как
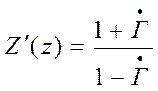 ,
,
то соответствует точке определяемой ![]() значение
значение
![]() , где
, где
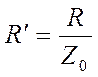 и
и 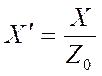 -
нормированные значения активного и реактивного сопротивлений.
-
нормированные значения активного и реактивного сопротивлений.
Круговая диаграмма находит широкое применение. С ее помощью можно определить коэффициент отражения и нормированное входное сопротивление в любом сечении волновода, если известны положение и величина нагрузки.
Также можно решить обратную задачу – зная КСВН и положение минимума
стоячей волны, определить либо, коэффициент отражения от нагрузки ![]() , либо сопротивление нагрузки
, либо сопротивление нагрузки ![]() , зная ее положение по длине волновода
, зная ее положение по длине волновода ![]() .
.
![]()
 |
||||||
|
||||||
|
||||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.