Синфазная вибраторная антенна. Директорная антенна или антенна «волновой канал». Линзовые антенны. Щелевые антенны, страница 2

Теоретический расчет токов в вибраторах довольно сложен. В принципе он ведется так же, как для п связанных контуров, путем решения системы из п уравнений Кирхгофа, аналогичных уравнениям для двух связанных вибраторов.

Диаграмма направленности директорной антенны, а также зависимость КНД от длины антенны  (п—полное число вибраторов) (рис. 37), и коэффициента замедления имеют вид, обычный для антенн с осевым излучением. То обстоятельство, что не все вибраторы антенны обладают одинаковой длиной, практического значения не имеет, так как форма диаграммы одиночного вибратора с изменением его длины меняется довольно мало. Также не существенно некоторое различие расстояния между вибраторами d_р и d_д, которые выбираются соответственно равными  и .

Отличительной чертой директорией антенны является ее узкополосность, как в отношении входных сопротивлений, так и в отношении направленных свойств. Сравнительно небольшая (~1%) расстройка частоты приводит к резкому изменениюраспределения тока в антенне и, следовательно, к искажению формы диаграммы направленности и рассогласованию входных сопротивлений с фидером питания.

Однако, простота и легкость конструкции этой антенны в ряде случаев является серьезным преимуществом, благодаря которому директорные антенны, несмотря на их узкополосность, находят широкое применение в качестве самостоятельных излучателей и элементов плоскостных синфазных антенн-решеток.

4. Спиральные антенны

Спиральные антенны представляют собой отрезок спирального волновода с замедленной бегущей волной, образованного спиральным проводником (рис. 38). Вдоль прохода спирали распространяется бегущая волна тока с коэффициентом замедления ξ_i, а волна поля распространяется вдоль оси спирали с коэффициентом замедления ξ, причем плоскость поляризации поля в спирали вращается в направлении намотки витков спирали. При этом поле в дальней зоне в направлении оси спирали также имеет вращающуюся поляризацию с коэффициентом эллиптичности, близким к единице.

Явление вращения плоскости поляризации   поля   спиральной антенны может быть объяснено следующим образом

Полное поле антенны представляется в виде суммы полей

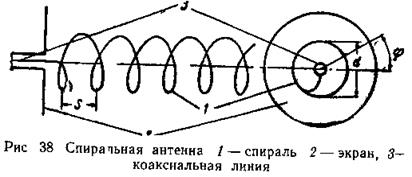
от всех одинаковых ее витков, причем каждый  отдельный виток спирали в осевом направлении имеет вращающееся поле.

Поэтому достаточно рассмотреть   поляризационные   свойства лишь одного витка  При анализе июля в осевом направлении виток удобнее представлять плоским, что не нарушает   качественной картины явления.

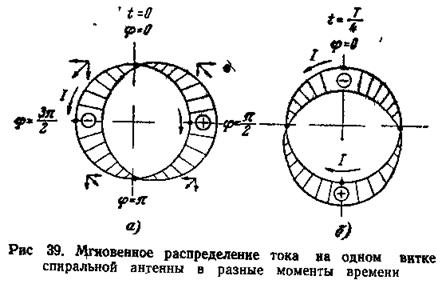
Проследим положение плоскости поляризации поля витка в течение полупериода высокочастотного колебания t= 0 ÷ Т/2.

В первой момент времени t=0 мгновенное распределение тока на витке, соответствующее бегущей волне, имеет вид, показанный на рис. 39, а. При этом предполагается, что полная длина витка равна длине волны для тока с учетом его замедления

Такой виток излучает поле в основном за счет вертикальных токов, так как они всюду имеют одно направление {рис 39, а), и их излучение суммируется. В то же время горизонтальные составляющие токов в верхней, нижней, левой и правой частях витка направлены противоположно и излучают слабо, а в осевом направлении вообще не излучают.

Таким образом, первому моменту времени соответствует вертикальное направление излучающих токов и вектора излученного поля .

За последующий период времени   t= 0 ÷ Т/4 волна тока на витке сдвинется на четверть длины волны, то есть на четверть оборота, и примет положение, показанное на рис 39, б. Вместе с этим повернется на 90° и направление основных излучающих токов, принявших теперь горизонтальное направление. Следовательно и плоскость поляризации поля также повернется за время четверти периода на угол 90°.

Продолжая рассуждения тем же путем, можно проследить дальнейшее вращение плоскости поляризации вектора , совершающего один полный оборот за период высокочастотного колебания T. Таким образом, поле, излученное витком с бегущей волной тока, действительно обладает круговой поляризацией в целом. Этим же свойством обладает и антенна. Благодаря распределению тока и поля вдоль спирали по закону бегущей волны, спиральные антенны обладают свойствами антенн с осевым излучением и круговой поляризацией в осевом направлении.