2.2 Расчет коробки балки жесткости.
Расчет коробки балки жесткости проводим с помощью программы “Ferma”. По полученным результатам проводим проверки по прочности и устойчивости. Помимо расчета балки жесткости можно провести расчет вант и пилона моста.
2.2.1 Исходные данные.
Расчетная схема.
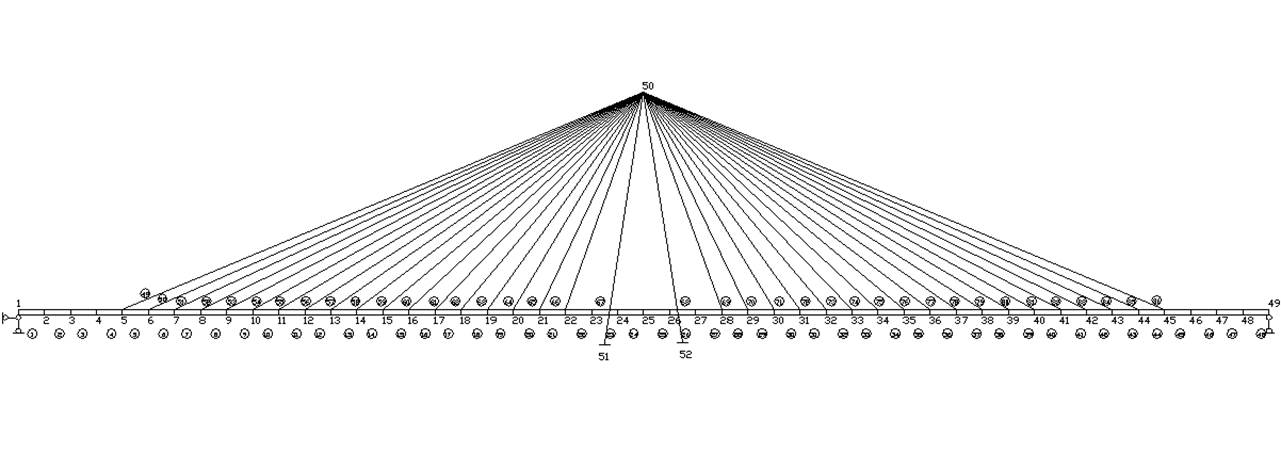
Рис. 11 “Расчетная схема моста”
Расчетные параметры
Постоянные нагрузки:
-
нормативная нагрузка 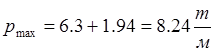 ;
;
-
максимальная нагрузка 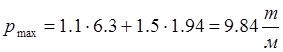 ;
;
-
минимальная нагрузка 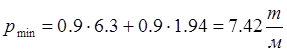 .
.
Коэффициент поперечной установки:
-
![]()
-
![]()
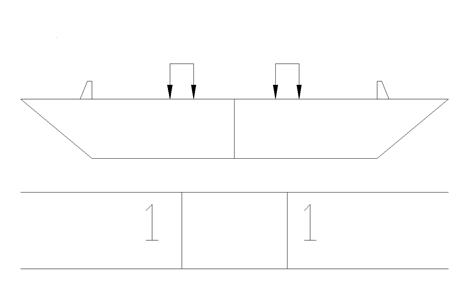
Рис.12 “Расчетная схеме при определении КПУ”
Геометрические характеристики:
-
пилон![]() ;
;
-
вант ![]() ;
;
-
балка жесткости ![]()
2.2.2 Проверка сечения балки жесткости по прочности.
Проверку сечения проводим в верхних волокнах по наибольшему изгибающему опорному моменту, в нижних волокнах по изгибающему моменту в нижних волокнах.
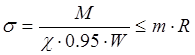 , где М –
максимальный изгибающий момент в балке;
, где М –
максимальный изгибающий момент в балке;
W – момент сопротивления сечения балки;
R – расчетное сопротивление стали, равное 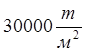
(по СНиП 2.05.03-84 “Мосты и трубы” с.73 п.4.7);
m – коэффициент условий работы, равный 1.0
(по СНиП 2.05.03-84 “Мосты и трубы” с.77 п.4.19);
Так же проводим расчет по касательным
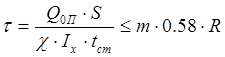
где Qоп – перерезывающая сила в опорном сечении;
tст – толщина стенки;
S, Ix – статический момент и момент инерции сечения балки;
R – расчетное сопротивление стали, равное 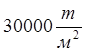
(по СНиП 2.05.03-84 “Мосты и трубы” с.73 п.4.7);
m – коэффициент условий работы, равный 1.0
(по СНиП 2.05.03-84 “Мосты и трубы” с.77 п.4.19);
и главным напряжениям
![]()
где sм – нормальные напряжения в стенке балки;
tм – касательные напряжения в стенке балки.

Рис.13 “Геометрические характеристики поперечного сечения балки”
- по нормальным напряжениям:
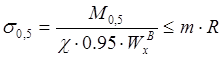
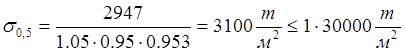 ;
;
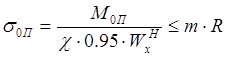
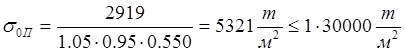
- по касательным напряжениям:
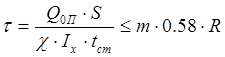
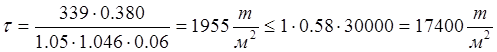
- по главным напряжениям:
![]()
sm=5023т/м2
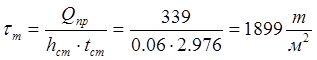
Тогда 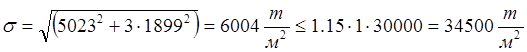
2.2.3 Проверка сечения балки на устойчивость.
Расчет поперечного сечения коробки ведем по следующей формуле:
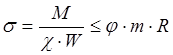 .
.
М – изгибающий момент в балке;
W – момент сопротивления балки;
R – расчетное сопротивление стали, равное 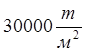
(по СНиП 2.05.03-84 “Мосты и трубы” с.73 п.4.7);
m – коэффициент условий работы, равный 1.0
(по СНиП 2.05.03-84 “Мосты и трубы” с.77 п.4.19);
j - коэффициент при расчете на устойчивость
(по СНиП 2.05.03-84 “Мосты и трубы” с.161 приложение15);
Свободна длина элемента ![]() .
.
Радиус инерции определяем из следующего соотношения:
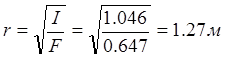 .
.
Гибкость элемента равна 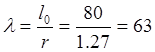 . По таблицам СНиП 2.05.03-84 “Мосты и
трубы” определяем коэффициент
. По таблицам СНиП 2.05.03-84 “Мосты и
трубы” определяем коэффициент![]() .
.
Тогда напряжения будут равны:
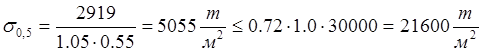 .
.
Уменьшение сечения балки не ведем из соображений возможных больших погибов системы в целом.
2.2.4 Расчет прикрепления балки жесткости.
Стык пролетного строения представляет собой комбинированное соединение. Полки балки свариваются между собой, стенка же соединяется при помощи накладок и болтов.
Максимальные усилия:
-
изгибающий момент ![]() ;
;
-
поперечная сила ![]() .
.
Схема стыка приведена на рис.14.
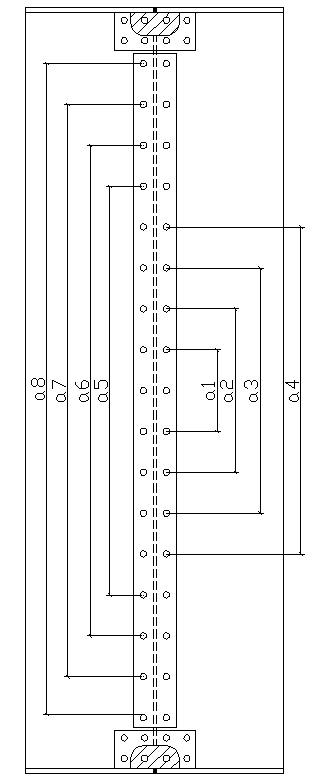
Рис.14. “Расчетный стык пролетного строения”
Количество болтов в стенке:
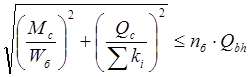 , где
, где 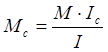 - изгибающий момент, приходящийся на
стенку, равный 450тм;
- изгибающий момент, приходящийся на
стенку, равный 450тм;
Wб – момент сопротивления болтового поля
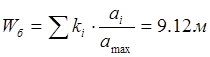 ;
;
Qbh – несущая способность одного болтоконтакта, равная 9.45тс.
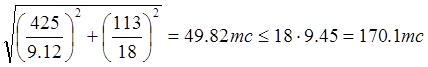 .
.
Таким образом количество болтов в стенке принимаем равным 18шт.
Пилон вантового мост рассчитываем как сжато-изогнутый стержень.
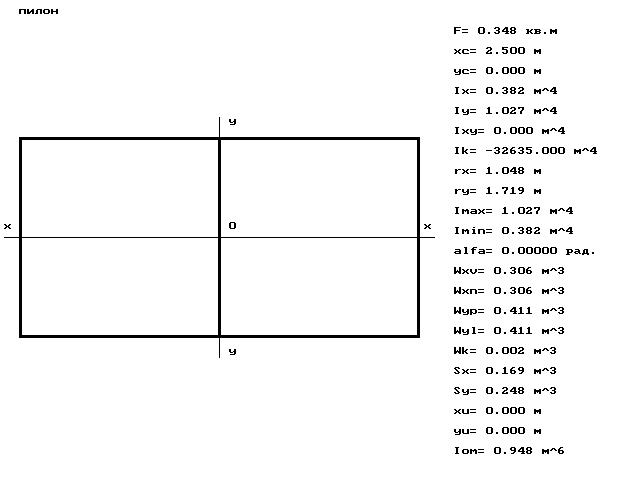
Рис. 15 “Расчетные характеристики пилона моста”
Проверку сечения по прочности проводим изгибающему моменту и продольному усилию:
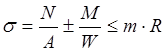 , где М –
максимальный изгибающий момент в пилоне;
, где М –
максимальный изгибающий момент в пилоне;
W – момент сопротивления сечения пилона;
N – продольная сила в пилоне;
А – площадь поперечного сечения пилона;
R – расчетное сопротивление стали, равное 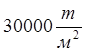
(по СНиП 2.05.03-84 “Мосты и трубы” с.73 п.4.7);
m – коэффициент условий работы, равный 1.0
(по СНиП 2.05.03-84 “Мосты и трубы” с.77 п.4.19);
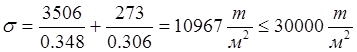 .
.
Расчет поперечного сечения коробки по устойчивости ведем по следующей формуле:
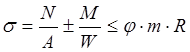 , где
М – максимальный изгибающий момент в пилоне;
, где
М – максимальный изгибающий момент в пилоне;
W – момент сопротивления сечения пилона;
N – продольная сила в пилоне;
А – площадь поперечного сечения пилона;
R – расчетное сопротивление стали, равное 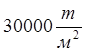
(по СНиП 2.05.03-84 “Мосты и трубы” с.73 п.4.7);
m – коэффициент условий работы, равный 1.0
(по СНиП 2.05.03-84 “Мосты и трубы” с.77 п.4.19);
j - коэффициент при расчете на устойчивость
(по СНиП 2.05.03-84 “Мосты и трубы” с.161 приложение15);
Свободна длина элемента ![]() .
.
Радиус инерции определяем из следующего соотношения:
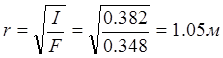 .
.
Гибкость элемента равна 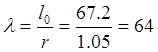 . По таблицам СНиП 2.05.03-84 “Мосты и
трубы” определяем коэффициент
. По таблицам СНиП 2.05.03-84 “Мосты и
трубы” определяем коэффициент![]() .
.
Тогда напряжения будут равны:
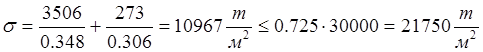 .
.
Подбор сечения вант проводим исходя из максимального усилия, полученного из программы FERMA. Вант рассчитывается как растянутый элемент. Максимальное усилие действующее в ванте равно 210т. Принимаем вант сечением 70мм с нормативным разрывным усилием равным 425т. Диаметр проволок принимаем равным 7мм.
Расчет на прочность канатов:
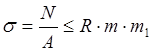 , где N
– усилие в канате;
, где N
– усилие в канате;
А – площадь поперечного сечения ванты;
R
– расчетное сопротивление каната, равное 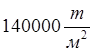 ;
;
m – коэффициент условий работы, равный 0.8
(по СНиП 2.05.03-84 “Мосты и трубы” с.77 п.4.19);
m1 – коэффициент условий работы, равный 1.0
(по СНиП 2.05.03-84 “Мосты и трубы” с.160 приложение 14);
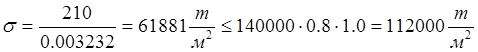 .
.
Уменьшение сечения вант не ведем из соображений возможных больших погибов системы в целом.
Величины прогибов определяем по программе FERMA,
подставляя полученные характеристики сечения балки жесткости, пилона и вант.
Предельный прогиб балки жесткости равен 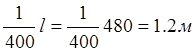 .
Максимальный прогиб полученный при расчете равен 1.12м, что укладывается в
установленные допуски.
.
Максимальный прогиб полученный при расчете равен 1.12м, что укладывается в
установленные допуски.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.