Разработка вариантов металлического моста под автодорогу. Расчет проезжей части

нормальное напряжение в месте сопряжения стенки с наиболее напряженным поясом

Касательные напряжения:

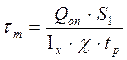
Статический момент инерции сечения, находящегося выше точки 1, относительно оси 1.

           

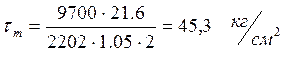
 - среднее касательное напряжение в стенке

Проверка ВЫПОЛНЕНА

                             2.1.3.   Расчет на выносливость продольного ребра

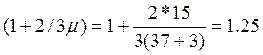
М0,5=γf1*pдпωm+γfν*(1+2/3μ)*ν*ωm+γfk*(1+2/3μ)*Pk*(y1+y2)=1*0,15*1,125+1*1,25*0,54*1,125+ +1*1,25*2,16*(0,75+0)=3,03 т*м

Qоп=γf1*pдпωq+γfν*(1+2/3μ)*ν*ωq+γfk*(1+2/3μ)*Pk*(y3+y4)=1*0,15*1,5+1*1,25*0,54*1,5+1* *1,25*2,16*(1+0,5)=5,245 т

Проверка на выносливость производиться по следующей формуле:

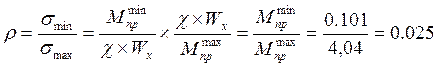
 - коэфф. ассиметрии цикла переменных напряжений

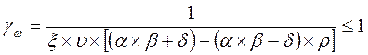
 - динамический коэфф. временной вертикальной нагрузке

 

 и  - коэфф., зависящие от марки стали; ,
      - эффективный коэфф. концентрации напряжений

 - коэфф., зависящий от длины загружения л.в.

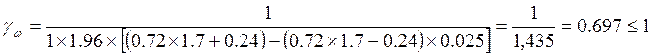
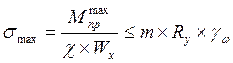
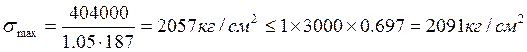
Проверка ВЫПОЛНЕНА - сечение удовлетворяет всем проверкам.

2.1.4.  Расчёт фрикционных соединений

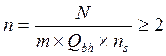,где

n - количество болтов в соединении при действии продольной силы N, равной

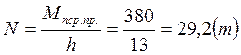
m=0.9- коэффициент условий работы

 - усилие, воспринимаемое одним «болтоконтактом», при числе 4 болтов во  фрикционном соединении

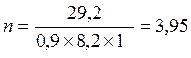 шт.

Принимаем 4 болта.

2.2.  Расчёт поперечных ребер

Расстояние между главными балками арочного пролётного строения составляет 9 м., соответственно, длину поперечных  рёбер ортотропной плиты примем равной 9 м. В расчёте не учитывается собственный вес поперечных и продольных балок, ввиду их малости.

                                            2.2.1. Усилия в поперечных рёбрах

Линия влияния давления на поперечное ребро приведена на рисунке.

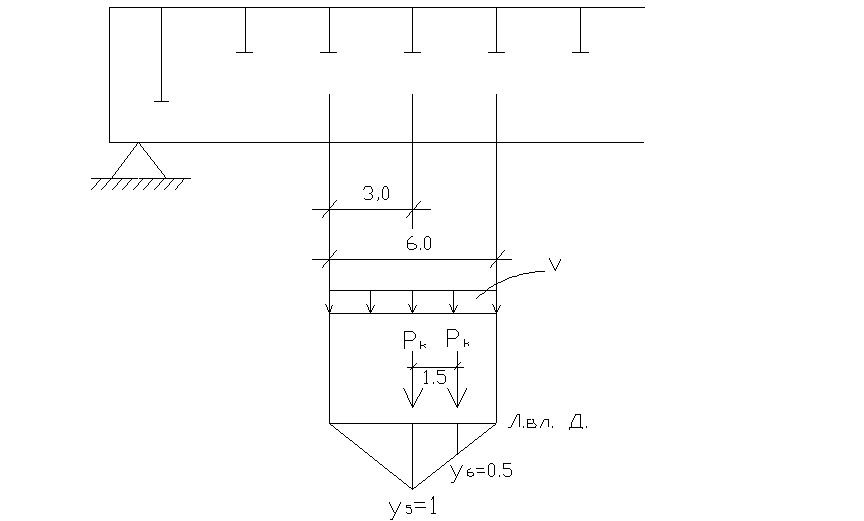
Величина давления на поперечное ребро определится по формуле:

Величинаравномерно распределённой нагрузки будет равна:

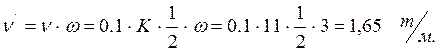
Вес дорожного покрытия, передаваемый на поперечное ребро равен:

Линии влияния момента и перерезывающей силы для поперечного ребра и схемы их загружения показаны на рисунке.

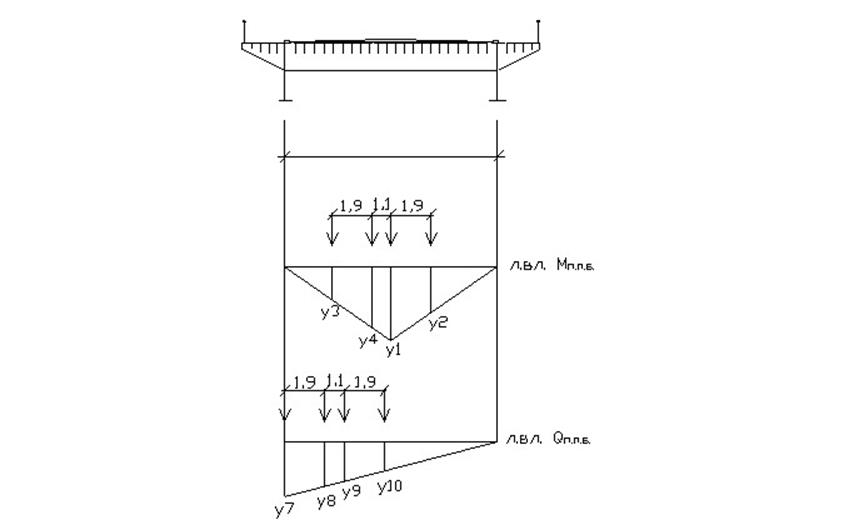
Загружая линию влияния для изгибающего момента в середине пролёта по соответствующей схеме, получаем следующее выражение:

Динамический коэффициент определяется по формуле:

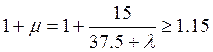
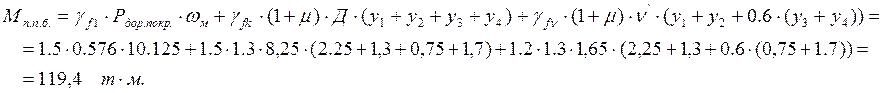
Выражение для перерезывающей силы в опорном сечении записывается в следующем виде:

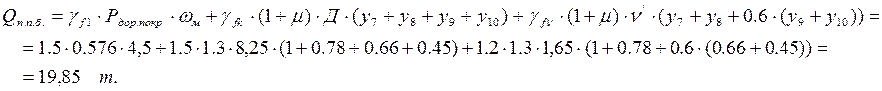
2.2.2. Геометрические характеристики сечения

Ширина верхнего листа поперечного ребра принимается равной величине расстояния между поперечными рёбрами, либо 0,2 от своей длины (выбирается меньшее). В нашем случае эта величина равна 2,4 м. Все остальные размеры поперечного сечения ребра представлены на рисунке.

Элемент сечения	Угол	Зеркально
Лист 1800 x 12	0 град	-
Лист 876 x 12	90 град	-
Лист 200 x 12	0 град	-

Габариты сечения 1800 x 900 мм

Геометрические характеристики сечения
	Параметр	Значение	Единицы измерения
A	Площадь поперечного сечения	345,12	см2
a	Угол наклона главных осей инерции	90	град
Iy	Момент инерции относительно центральной оси Y1 параллельной оси Y	329806,478	см4
Iz	Момент инерции относительно центральной оси Z1 параллельной оси Z	584012,614	см4
It	Момент инерции при свободном кручении	156,63	см4
iy	Радиус инерции относительно оси Y1	30,913	см
iz	Радиус инерции относительно оси Z1	41,136	см
Wu+	Максимальный момент сопротивления относительно оси U	6489,029	см3
Wu-	Минимальный момент сопротивления относительно оси U	6489,029	см3
Wv+	Максимальный момент сопротивления относительно оси V	4731,734	см3
Wv-	Минимальный момент сопротивления относительно оси V	16247,404	см3
Wpl,u	Пластический момент сопротивления относительно оси U	9871,536	см3
Wpl,v	Пластический момент сопротивления относительно оси V	8947,707	см3
Iu	Максимальный момент инерции	584012,614	см4
Iv	Минимальный момент инерции	329806,478	см4
iu	Максимальный радиус инерции	41,136	см
iv	Минимальный радиус инерции	30,913	см
ym	Координата центра масс по оси Y	90	см
zm	Координата центра масс по оси Z	-20,299	см

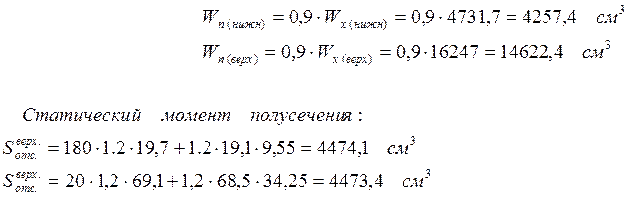
Расчёт по касательным напряжениям ведём по максимальному значению статического момента полусечения.

                      2.2.3. Проверка прочности поперечного ребра

Максимальное нормальное напряжение в середине пролёта ребра:

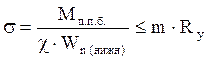
где χ – принимаем равным 1.05

m – принимаем равным  1, для автодорожных мостов.

Ry – расчётное сопротивление стали растяжению (15ХСНД – 30000  )

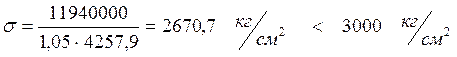
Касательные напряжения по нейтральной оси в надпорном сечении:

     

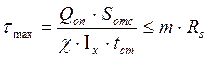
где Rs – расчётное сопротивление стали сдвигу.

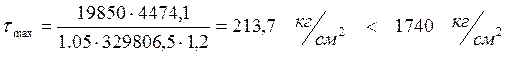
2.2.4. Проверка выносливости поперечного ребра

Проверка на выносливость осуществляется по той же методике, что и расчёт по прочности, но все коэффициенты γ в формулах для определения изгибающих моментов и перерезывающих сил, принимаются равными 1, значение динамического коэффициента определяется по формуле:

                                                            

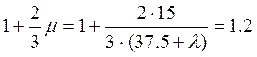
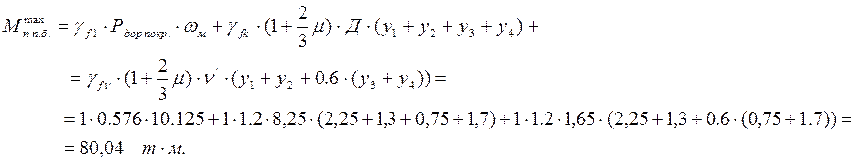
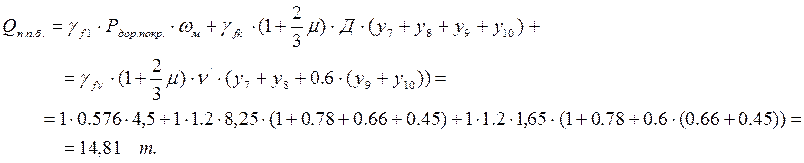
Проверка на выносливость производиться по следующей формуле:

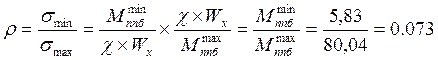
 - коэфф. ассиметрии цикла переменных напряжений

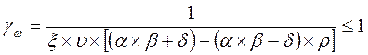
 - динамический коэфф. временной вертикальной нагрузке

 

 и  - коэфф., зависящие от марки стали; ,
      - эффективный коэфф. концентрации напряжений

 - коэфф., зависящий от длины загружения л.в.

 

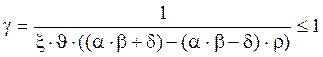
где ξ – коэффициент равный 0,7 для автодорожных и городских мостов;

- коэффициент, зависящий от длины загружения λ линии влияния и равный 1,61 

α и δ – коэффициенты, зависящие от марки стали и равные соответственно 0,72 и 0,24.

 - эффективный коэфф. концентрации напряжений   

ρ – характеристика цикла переменных напряжений.

 

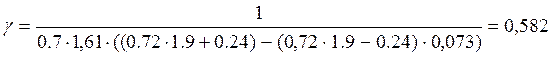
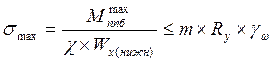
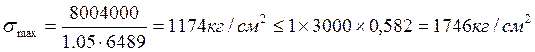
Проверка ВЫПОЛНЕНА - сечение удовлетворяет всем проверкам.

2.1.4.  Расчёт фрикционных соединений

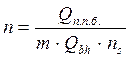,где

n - количество болтов в соединении при действии продольной силы N, равной                                                     

m=0.9- коэффициент условий работы

 - усилие, воспринимаемое одним «болтоконтактом», при числе 4 болтов