Изучение равномерного движения материальной точки в плоскости по криволинейной траектории, страница 2

 

	N

	C

Пояснения к другим величинам были даны выше.

III.  Решение поставленных задач

1. Обоснование применения законов, уравнений и соотношений, используемых при решении.

Все описанные в кратких теоретических сведениях законы можно применить в условиях данной задачи, т.к. ее физическая модель удовлетворяет границам применимости этих законов.

2. а) 1)  парабола

              первая производная у по х

 вторая производная у по х

 первая производная в точке x=0

  вторая производная  в точке x=0

2) 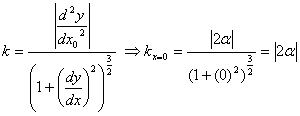 кривизна y=f(x) в точке x=0

Радиус кривизны в точке x=0: 

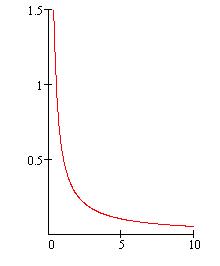
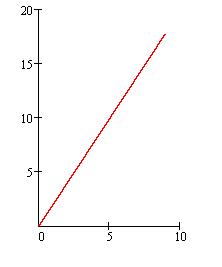
График зависимости y=R():

3) Полное ускорение частицы в точке x=0 будет равно нормальному ускорению в этой точке:

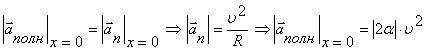
График зависимости y=a():

4) В общем виде кривизна кривой в точке будет вычисляться как 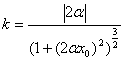 , радиус кривизны как  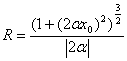 и ускорение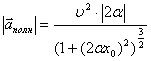 

б) 1)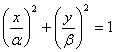

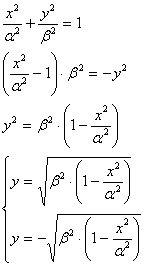
Для случая 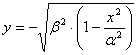 вид производных сохраняется, только их надо умножить на -1, но это не имеет существенного значения, потому что в формуле кривизны « - » уничтожают квадрат и модуль.

1)

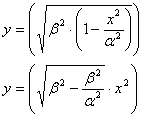
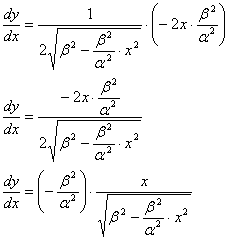
2)

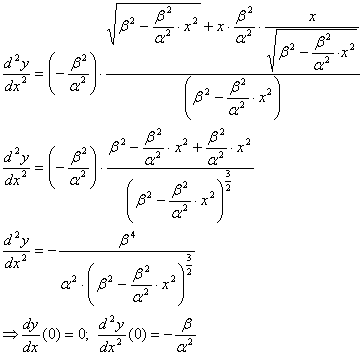
Кривизна k в точке  x=0 будет равна:  радиус кривизны в точке x=0   будет равен: 

График зависимости :

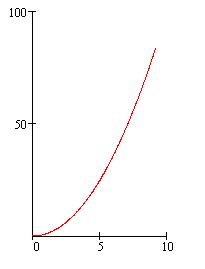
График зависимости :