Изучение равномерного движения материальной точки в плоскости по криволинейной траектории

I.  Задание в соответствии с вариантом

Частица движется равномерно со скоростью  по плоской траектории y(x). Найти ускорение частицы в точке x=0  и радиус кривизны траектории в этой точке, если траектория:

а) парабола

б) эллипс 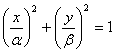, где  постоянные.

Построить график зависимости ускорения частицы и радиуса кривизны траектории от коэффициентов .

II.  Краткое теоретическое содержание

1.  Явление, изучаемое в РГР

В РГР изучается равномерное движение материальной точки в плоскости по криволинейной траектории.

2.  Определение основных физических понятий, объектов, процессов и величин.

Материальная точка – это тело, обладающее массой, формой и размерами которого в данной задаче можно пренебречь.

Скоростью материальной точки называется предел средней скорости  при , т.е. производная от радиуса-вектора  по времени :

Вектор скорости направлен по касательной к траектории точки в сторону ее движения.

Равномерное движение – это такое движение, при котором за любые равные промежутки времени тело проходит равные участки пути.

Ускорением материальной точки называется предел среднего ускорения  при , т.е. производная от вектора скорости  по времени: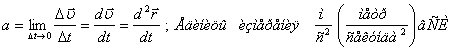

Траектория движения материальной точки – это линия, которую описывает эта точка при своем движении.

Криволинейное движение тела – это такое движение тела, при котором его траектория движения отлична от прямой линии.

Любое криволинейное движение можно представить как движение по отрезкам и(или) дугам окружностей.

Кривизна плоской линии (не по определению). Если линия задана уравнением y=f(x), то ее кривизна вычисляется по формуле: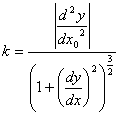

Радиус кривизны – величина, обратная кривизне:

3. Законы и соотношения, описывающие изучаемые процессы.

Модуль полного ускорения материальной точки может быть представлен как корень из суммы квадратов тангенциального и нормального ускорений: 

Тангенциальное ускорение отвечает за изменение модуля скорости, а нормальное ускорение отвечает за изменение направления скорости.

В случае равномерного движения по криволинейной траектории тангенциальное ускорение равно 0, нормальное же ускорение в каждой точке траектории можно вычислить таким образом , где  - это скорость тела в точке, а  - радиус кривизны траектории в этой точке.

4.  Пояснения к физическим величинам, входящим в формулы, и единицы их измерения.

(кривизна траектории в некоторой точке M) – это предел отношения угла поворота  касательной к длине дуги S (MN), при , т.е.  . Единицей измерения кривизны кривой в точке служит .