Электроника: Рабочая программа. Методические указания к практическим занятиям. Задания на контрольную работу, страница 10

Задача 14.  Произвести суммирование (вычитание) двух аналоговых сигналов  и . Определить ограничения величин возможных изменений

этих сигналов с тем, чтобы сумматор (вычитатель) работал в линейном режиме и не искажал результат арифметического действия. Известна схема сложения (вычитания), в состав которой входят следующие элементы: масштабные резисторы и операционный усилитель с определёнными величинами напряжений питания  и .

Методические рекомендации

Схемы сложения и вычитания на операционном усилителе в разных режимах включения показаны на рис.32 … 35.

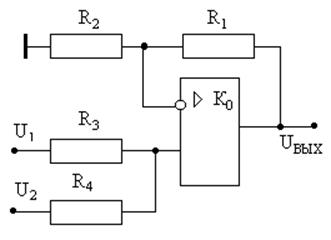
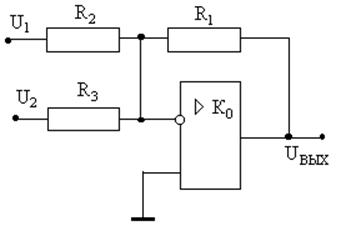
Рис. 32                                                     Рис. 33

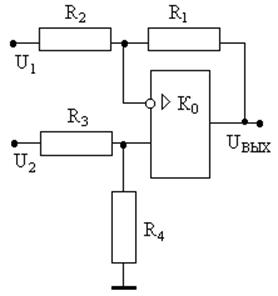
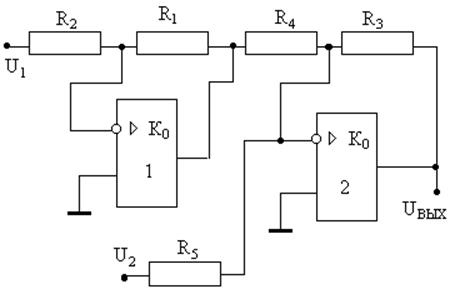
Рис.34                                                   Рис.35

Суммирование на усилителе-повторителе (рис.32) входных напряжений  и  происходит на прямом входе усилителя. При этом выходное напряжение .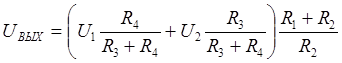

Сложение входных напряжений на инвертирующем входе усилителя-инвертора (рис. 33) формирует выходное напряжение, равное

 .

При дифференциальном включении усилителя (рис. 34)  для сложения или вычитания входных напряжений  и  напряжение на выходе усилителя  .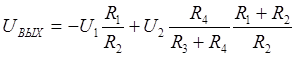

Максимальное значение суммарного сигнала на входе усилителя, при котором он работает ещё в линейном режиме, т. е. когда выходное напряжение ещё не достигает максимального значения, равного  или , называется динамическим диапазоном усилителя. Для операционного усилителя динамический диапазон  исчезающе мал - 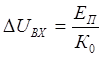, так как коэффициент его усиления  очень велик. Для ОУ с отрицательной обратной связью динамический диапазон больше, так как определяется уже меньшим вследствие действия обратной связи коэффициентом усиления:   или  .  Знаки «+» и «-» означают, в какой области напряжений – положительной или отрицательной - изменяется выходное напряжение при воздействии входного сигнала.

В схемах, изображенных на рис.32 … 34, сумма входных сигналов  и   не должна выходить за пределы динамического диапазона.

Для того чтобы увеличить диапазон возможных величин входных напряжений, которые необходимо складывать или вычитать, применяют каскадное включение ОУ. К примеру, применение двух усилителей-инверторов (рис.35) позволяет получить разность двух однополярных напряжений, максимальные значения каждого из которых соответствуют пределу динамического диапазона применяемых операционных усилителей. В этой схеме напряжение на выходе усилителя 1  равно

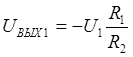 ,  а на выходе усилителя 2 -    .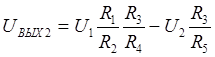

     Задача 15.  Для компаратора (рис.36) на основе операционного усилителя из предыдущей задачи рассчитать момент сравнения   и ошибку момента сравнения  (рис.37), вызванную его разрешающей способностью, если известно, что на инвертирующий вход подается линейно изменяющееся напряжение со скоростью , а на неинвертирующий  вход - опорное напряжение , значения которого задаются в табл. 1. Все остальные данные, необходимые для расчета , взяты из предыдущей задачи.

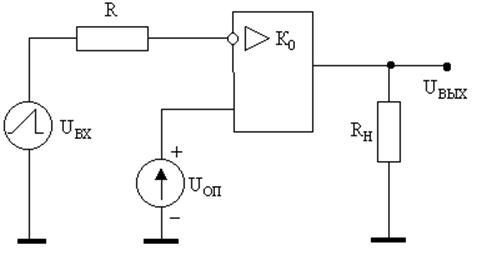
Рис.36

Методические рекомендации

Задать необходимые исходные данные для расчетов:       ,    ,         ,        ,        .

Определить зону неопределённости сравнения ,  вызванную конечной величиной коэффициента усиления ОУ, . Ширина этой зоны характеризует чувствительность или разрешающую способность компаратора:

.

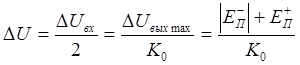Рассчитать время до момента сравнения, в течение которого напряжение  изменяется от 0 до , и ошибку определения момента сравнения , причиной которой является разрешающая способность компаратора по выражениям            .

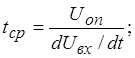
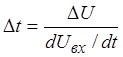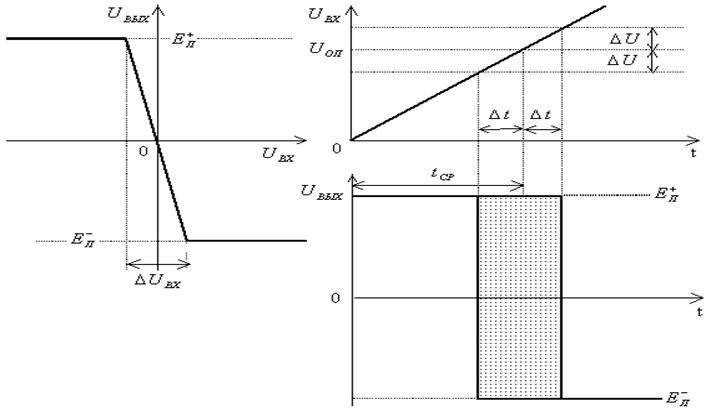
а)                                                 б)

Рис.37

Выполнив анализ передаточной характеристики и временных диаграмм, изображенных на рис. 37, определить, что нужно предпринять, чтобы уменьшить ошибку момента сравнения.

2.4.Практическое занятие 4

Анализ и синтез цифровых автоматов без памяти

Цели занятия:  1. Ознакомить обучаемых с процедурами анализа и синтеза цифровых автоматов без памяти.

2. Подготовить обучаемых к выполнению контрольных заданий по анализу и синтезу комбинационных схем.

Анализ автоматов без памяти

Задача анализа автоматов формулируется так. Задана структурная схема автомата, построенная на элементарных автоматах, образующих основную функционально полную систему двоичных функций. Необходимо определить функцию, реализуемую автоматом.