Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
СЕВЕРО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ ЗАОЧНЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Специальность: 100400 Курс 4
Форма обучения: очно − заочная
Шифр
Оценка
Подпись преподавателя
«____»________200 г.
Задача 1. Рассчитать фазные и линейные ЭДС трёхфазной синхронной машины при соединении фаз звездой с учётом первой, третьей, пятой и седьмой гармонических составляющих при частоте f = 50 Гц и следующих данных: максимальная индукция Вδ = 0,9 Тл; число пазов z = 96; число пар полюсов р = 4; сокращение шага β = 5/6; полюсная дуга τ = 80 см; активная длина проводника l = 20 см: число витков в одной ветви фазы w = 20.
Решение:
Число
пазов на полюс и фазу 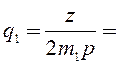
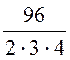 = 4.
= 4.
Коэффициенты распределения:
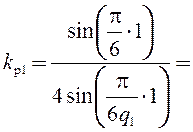 0,958;
0,958;
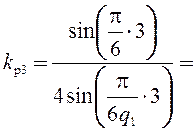 0,653;
0,653;
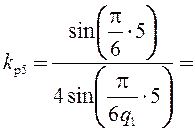 0,205;
0,205;
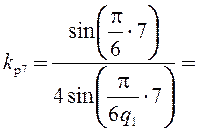 −0,158.
−0,158.
Коэффициенты укорочения:
kу1 = sin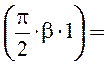 0,966;
0,966;
kу3 = sin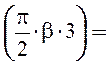 −0,707;
−0,707;
kу5 = sin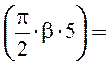 0,259;
0,259;
kу7 = sin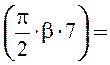 0,259.
0,259.
Полные обмоточные коэффициенты:
kw1 = kp1ky1 = 0,958∙0,966 = 0,925;
kw3 = kp3ky3 = 0,653∙(−0,707) = −0,462;
kw5 = kp5ky5 = 0,205∙0,259 = 0,053;
kw7 = kp7ky7 = (−0,158)∙0,259 = −0,041.
Частота каждой из гармонических составляющих:
f1 = f·1 = 50 Гц;
f3 = f·3 = 150 Гц;
f5 = f·5 = 250 Гц;
f7 = f·7 = 350 Гц.
Полюсные дуги каждой из гармонических составляющих:
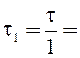 0,8 м;
0,8 м;
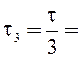 0,8/3 = 0,267 м;
0,8/3 = 0,267 м;
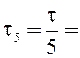 0,8/5 = 0,16 м;
0,8/5 = 0,16 м;
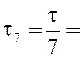 0,8/7 = 0,114 м.
0,8/7 = 0,114 м.
Амплитуды индукций в воздушном зазоре каждой из гармонических составляющих:
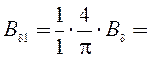 4∙0,9/3,142 = 1,146 Тл;
4∙0,9/3,142 = 1,146 Тл;
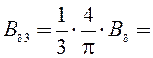 4∙0,9/3∙3,142 = 0,382 Тл;
4∙0,9/3∙3,142 = 0,382 Тл;
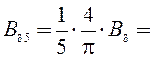 4∙0,9/5∙3,142 = 0,229 Тл;
4∙0,9/5∙3,142 = 0,229 Тл;
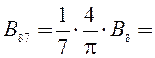 4∙0,9/7∙3,142 = 0,164 Тл.
4∙0,9/7∙3,142 = 0,164 Тл.
Магнитный поток для каждой из гармонических составляющих:
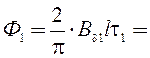 2∙1,146∙0,2∙0,8/3,142 = 0,117 Вб;
2∙1,146∙0,2∙0,8/3,142 = 0,117 Вб;
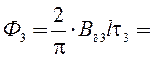 2∙0,382∙0,2∙0,267/3,142
= 0,013 Вб;
2∙0,382∙0,2∙0,267/3,142
= 0,013 Вб;
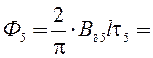 2∙0,229∙0,2∙0,16/3,142
= 4,669∙10−3 Вб;
2∙0,229∙0,2∙0,16/3,142
= 4,669∙10−3 Вб;
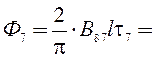 2∙0,164∙0,2∙0,114/3,142
= 2,382∙10−3 Вб.
2∙0,164∙0,2∙0,114/3,142
= 2,382∙10−3 Вб.
Фазные ЭДС для каждой гармонической составляющей:
Е1 = 4,44kw1wf1Ф1 = 4,44∙0,925∙20∙50∙0,117 = 479,393 В;
Е3 = 4,44kw3wf3Ф3 = 4,44∙(−0,462)∙20∙150∙0,013 = −79,799 В;
Е5 = 4,44kw5wf5Ф5 = 4,44∙0,053∙20∙250∙4,669∙10−3 = 5,508 В;
Е7 = 4,44kw7wf7Ф7 = 4,44∙(−0,041)∙20∙350∙2,382∙10−3 = −3,019 В.
Линейная
ЭДС: Ел = ![]()
![]() 830,405 В.
830,405 В.
В линейную ЭДС при соединении фаз звездой не входят гармоники, кратные трём.
Задача 2. В трехфазную сеть напряжением Uс = 10 кВ включен потребитель мощностью Sпотр = 4,5 кВА при коэффициенте мощности cosφ1 = 0,72. Определить мощность синхронного компенсатора Qск, который следует подключить параллельно потребителю, чтобы коэффициент мощности в сети повысился до значения cosφ′1 = 0,92.
Решение:
Реактивная мощность потребителя при cosφ1 = 0,72 Q = Sпотрsinφ1 = 4500∙0,69397 = 3123 ВАр.
Реактивная мощность потребителя при cosφ′1 = 0,92 Q′ = Sпотрsinφ′1 = 4500∙0,39192 = 1764 ВАр.
Реактивная мощность синхронного компенсатора Qск = Q – Q′ = Sпотр(sinφ1 – sinφ′1) = 3123 – 1764 = 1359 ВАр.
Задача 3. Генератор параллельного возбуждения имеет следующие данные: номинальное напряжение Uн = 220 B, число пар полюсов р = 2, скорость вращения п = 1500 об/мин. Определить потери и КПД. Исходные данные: Рн = 25 кВт, Iн = 130,8 А, Da = 210 мм, la = 165 мм, z = 27, hп = 27 мм, а = 1, N = 162, Sa = 0,00525 м2, La = 0,66 м, Sз0 = 0,00192 м2, bз0 = 0,0125 м, αi = 0,63.
Решение:
Потери на трение в подшипниках и вентиляционные выбираем из соотношения при Dа = 210 мм и п = 1500 об/мин → рмех ≈ 182 Вт.
Сечение щёток: Sщ ≈ 2∙10-5Iн = 2∙10-5∙130,8 = 2,616∙10-3 м2.
Окружная
скорость якоря: 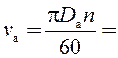 3,142∙0,21∙1500/60 = 16,493
об/мин.
3,142∙0,21∙1500/60 = 16,493
об/мин.
Потери на трение щёток о коллектор: рщ = 3500Sщvа = 3500∙2,616∙10-3∙16,493 = 151,013 Вт.
Номинальный ток возбуждения: Iвн = kвIн = 0,027∙130,8 = 3,532 А, где kв − выбирается из таблицы при Рн = 25 кВт.
|
Рн, кВт |
15 |
20 |
25 |
32 |
50 |
70 |
75 |
100 |
125 |
200 |
|
kв |
0,029 |
0,028 |
0,027 |
0,026 |
0,024 |
0,022 |
0,022 |
0,021 |
0,02 |
0,02 |
Номинальный ток якоря: Iaн = Iн + Iвн = 130,8 + 3,532 = 134,332 А.
Ra = 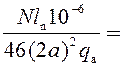 162∙0,356∙10-6/46∙16∙1,308∙10-5
= 0,027 Ом.
162∙0,356∙10-6/46∙16∙1,308∙10-5
= 0,027 Ом.
Длина проводника якоря: ln = la + lл = 0,165 + 0,231 = 0,396 м.
Длина
лобовой части проводника якоря: 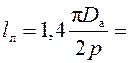 1,4∙3,142∙0,21/4 = 0,231 м.
1,4∙3,142∙0,21/4 = 0,231 м.
Сечение
проводника якоря: qa
= 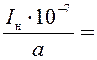 130,8∙10-7/1 = 1,30∙10-5 м2.
130,8∙10-7/1 = 1,30∙10-5 м2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.