Согласно этой функции, предложение сократится, то есть график предложения сместится вверх на 2у.е. и влево по горизонтали на 10 единиц. Функция спроса не изменится. Определим новое равновесие:
80-5P = 20+5Pt Pd = Pst =6; Qd = Qs = 50.
 Цена
S1 S Таким
образом, равновесное количеP D
ство покупаемой продукции сократи7
лось
и цена повысилась. Обратите вни6 потери
мание, что цена возросла на меньшую
Цена
S1 S Таким
образом, равновесное количеP D
ство покупаемой продукции сократи7
лось
и цена повысилась. Обратите вни6 потери
мание, что цена возросла на меньшую
5 покупателей величину, чем налог, в результате дейпотери ствия механизма рынка.
4 продавцов Объем налоговых поступлений от потоварного налога равен произведению величины налога на продаваемое ко20 30 50 55 80 Q личество товара: T = t*Qet = 2*50=100.
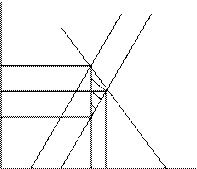
Установление налога ведет к потерям и для продавцов и для покупателей. Потери покупателей. Ранее объем 50 потребители покупали по цене 5у.е. Их расходы были равны 50*5=250у.е. Теперь они за этот объем платят 50*6=300у.е. Их потери составляют -50у.е.
Потери продавцов. Ранее продавцы продавали объем 50 по цене 5у.е. и получали доход 250у.е. Теперь они получают доход 300у.е. от продажи 50 единиц по цене 6у.е. Казалось бы, их доходы возросли. Но с каждой проданной единицы продавцы должны заплатить 2у.е., то есть общую сумму 100у.е. В результате реальная цена продажи для них составит 4у.е., и их фактический доход от продажи 50 единиц составит 200у.е., что на 50у.е. меньше, чем до введения налога (это их потери).
В данном примере налоговое бремя распределилось одинаково, что следует из расчетов и видно по графику. Это связано с одинаковой эластичностью спроса и предложения (что показывает коэффициент при независимой переменной в функции спроса и предложения). Если эластичность спроса более высокая, то налоговое бремя в основном падает на продавцов. Если эластичность предложения более высокая, то налоговое бремя падает в большей степени на покупателей.
На графике потери эффективности для общества показаны заштрихованным треугольником. Это тот объем продукции, который не был произведен и его не смогли приобрести покупатели, и тот объем доходов, который не получили продавцы.
Задача 2. Величина спроса на фрукты задана уравнением Qd=20 – 2P, величина предложения Qs = 2 + P.
1) Определите равновесную цену и объем продаж аналитически, по графику и по таблице.
2) На основе данной функции спроса определите, как изменяется эластичность спроса при снижении цены - по показателю общей выручки.
3) Определите, достигается ли при данном равновесном количестве максимальная выручка?
4) Как изменится выручка продавца, если предложение возрастет на 3 единицы? на 5 единиц?
5) Рассчитайте эластичность спроса по коэффициенту эластичности (дуговой и точечной).
Решение. 1) Равновесная цена – цена, уравновешивающая спрос и предложение в результате действия конкурентных сил. В условиях равновесия величина спроса равна величине предложения, цена спроса равна цене предложения. Для аналитического решения приравняем функцию спроса и функцию предложения и найдем равновесную цену:
Qd = Qs 20 - 2p= 2 + p 20-2=2р+р
18 =3р р = 6 рублей.
Подставим значение цены в функцию спроса или в функцию предложения и определим равновесное количествоQd = Qs = 8 единиц.
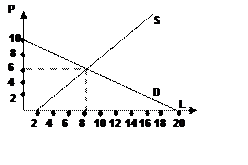 Графически равновесие – это
точка пересечения графиков спроса и предложения. Отметим по вертикальной оси
значения цены, по горизонтальной оси – количество продукции и построим графики
спроса и предложения по данным линейным функциям. График спроса будет выглядеть
как прямая нисходящая линия. Крайние точки – это цена P=10, при которой величина спроса Qd =0, и количество Qd= 20, при ценеP=0. Кроме того, отмечаем
точку равновесия P=6,Qd =8. График предложения
выглядит как прямая восходящая линия. Для построения отмечаем точку на
горизонтальной оси - величину предложения Qs =2 при цене P=0 и равновесную точку P=6,Qs =8. Графики пересекаются в точке равновесия.
Графически равновесие – это
точка пересечения графиков спроса и предложения. Отметим по вертикальной оси
значения цены, по горизонтальной оси – количество продукции и построим графики
спроса и предложения по данным линейным функциям. График спроса будет выглядеть
как прямая нисходящая линия. Крайние точки – это цена P=10, при которой величина спроса Qd =0, и количество Qd= 20, при ценеP=0. Кроме того, отмечаем
точку равновесия P=6,Qd =8. График предложения
выглядит как прямая восходящая линия. Для построения отмечаем точку на
горизонтальной оси - величину предложения Qs =2 при цене P=0 и равновесную точку P=6,Qs =8. Графики пересекаются в точке равновесия.
Для решения в табличной форме необходимо заполнить таблицу, отмечая в ней изменение величины спроса Qd и величины предложения Qs при изменении (снижении) цены. В таблице принято указывать изменение цены, начиная от максимальной до P = 0. Максимально высокая цена – это цена, при которой величина спроса Qd=0. Соответственно, при нулевой цене величина спроса максимальна. По функции спроса находим, что величина спроса Qd = 0, когда P = 10. Далее, на каждую единицу снижения цены величина спроса возрастает на 2 единицы, в соответствии с коэффициентом при независимой переменной (цене). При цене P = 0 величина спроса Qd =20 (max). Величина предложения при снижении цены на одну единицу снижается с учетом коэффициента, данного в функции, также на одну единицу.
При цене P=6руб. установится равновесие, то есть величина спроса равна величине предложения Qd = Qs = 8 единиц.
|
Цена P, руб. |
Величина спроса Qd, ед. |
Величина предложения Qs ед. |
Величина предложения |
Общая выручка TR= P*Q |
Коэффициент эластичности спроса ED |
||
|
Qs+3 ед. |
Qs+6ед. |
∆Q%/ ∆P% |
∆Q/∆P* P/ Q |
||||
|
10 |
0 |
12 |
15 |
18 |
0 |
∞ |
|
|
9 |
2 |
11 |
14 |
17 |
18 |
19 |
9 |
|
8 |
4 |
10 |
13 |
16 |
32 |
5,7 |
… |
|
7 |
6 |
9 |
12 |
15 |
42 |
… |
… |
|
6 |
8 |
8 |
11 |
14 |
48 |
1,85 |
1,5 |
|
5 |
10 |
7 |
10 |
13 |
50 |
1,2 |
1 |
|
4 |
12 |
6 |
9 |
12 |
48 |
0,8 |
… |
|
3 |
14 |
5 |
8 |
11 |
42 |
… |
… |
|
2 |
16 |
4 |
7 |
10 |
32 |
… |
… |
|
1 |
18 |
3 |
6 |
9 |
18 |
… |
0,1 |
|
0 |
20 |
2 |
5 |
8 |
0 |
0,05 |
0 |
2) Эластичность спроса – степень реакции потребителей на изменение цены. Эластичность спроса при линейной функции спроса не остается постоянной величиной. При последовательном снижении цены и движении по графику спроса вниз, эластичность спроса снижается, спрос из эластичного превращается в неэластичный.
Эластичность спроса можно определить по общей выручке TR=P*Q. Если при снижении цены TR растет, то спрос эластичный, снижать цену и увеличивать производство выгодно. Если при снижении цены TR снижается, то спрос неэластичный. Внесем показатели общей выручки TR в таблицу.
3) По таблице видно, что равновесие достигается на участке эластичного спроса, но выручка при данной функции спроса TR=P*Q=6*8=48 не максимальна, то есть возможно дальнейшее снижение цены
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.