Определение количества рейсов для двух типов самолетов авиакомпании, учитывая ограничения на количество пассажиров и размер фонда рабочего времени

Министерство Образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

Высшего профессионального образования

Магнитогорский государственный технический университет

им. Г.И. Носова

Кафедра промышленного транспорта.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

по дисциплине:

 «Методы оптимизации транспортных процессов»

Выполнила: Анисимова Ю. А.                                                                                          

Группа: ГТ-05-2

Проверили: доцент, к. т. н. Цыганов А. В.

доцент, к. т. н. Рахмангулов А. Н.

Магнитогорск 2007

Содержание

Введение. 3

1.Дискриптивные модели. 4

2. Графоаналитический метод решения простейших оптимизационных моделей. 5

3. Симплексный метод решения линейных математических моделей. 6

4. Симплексный метод с искусственным базисом.. 7

5. Построение и решение линейных оптимизационных моделей. 9

6. Решение транспортной задачи линейного программирования в матричной постановке методом потенциалов. 10

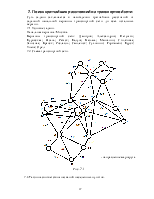
7. Поиск кратчайших расстояний на транспортной сети. 17

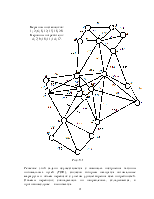
8. Решение транспортной задачи в сетевой постановке методом сокращения невязки. 19

9. Расчет оптимального варианта плана формирования поездов. 31

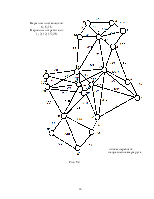
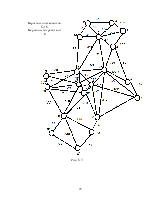
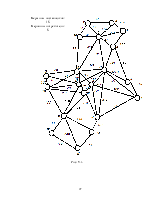
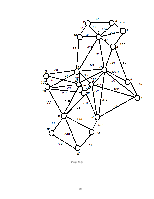
10. Решение «задаче коммивояжера» методом.. 33

«ветвей и границ». 33

11. Решения задачи этапного распределения ресурсов методом динамического программирования. 38

Заключение. 43

Приложение к  «задаче коммивояжера». 44

Введение

С конца ХХ века резко увеличилась сфера использования вычислительной техники во всех областях человеческой деятельности, в том числе и на транспорте. До появления персональных компьютеров круг задач, сводился к автоматизации учета, проектирования и выполнения плановых расчетов. Специалистам требовалось умение строить математическую модель производства или транспортного процесса, знание математических методов, позволяющих найти оптимальное решение.

Потребность в применении этих методов очень велика. Особенно это касается транспорта, где существует потребность решения сложных оптимизационных задач планирования и управления. Проблемы с выбором оптимальных решений существуют у железнодорожных и автотранспортных диспетчеров, работников плановых и технических отделов, в конструкторском бюро. Всем этим специалистам ежедневно приходится сталкиваться с проблемой выбора единственно правильного решения среди множества менее выгодных или невыгодных вообще.   

При увеличении числа компьютеров на рабочих местах и появлении программного обеспечения решать задачи управления и оптимизации можно на каждом рабочим месте инженера-транспортнака.

Реализация этих проблем на практике требует соответствующей подготовки инженеров, которые бы могли видеть производственную задачу, формулировать математическую модель, а затем решать ее с помощью приведенных ниже методов.

В данной работе представлены математические модели транспортных и производственных процессов, подробное решение оптимизационных задач «вручную», а также с применением персонального компьютера.       

1.Дискриптивные модели

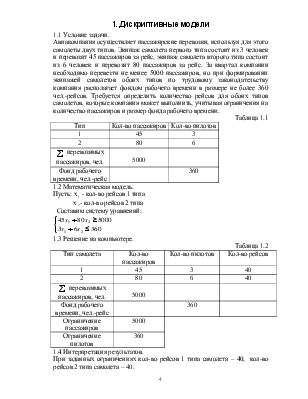
1.1 Условие задачи.

Авиакомпания осуществляет пассажирские перевозки, используя для этого самолеты двух типов. Экипаж самолета первого типа состоит из 3 человек и перевозит 45 пассажиров за рейс, экипаж самолета второго типа состоит из 6 человек и перевозит 80 пассажиров за рейс. За квартал компании необходимо перевезти не менее 5000 пассажиров, но при формировании экипажей самолетов обоих типов по трудовому законодательству компания располагает фондом рабочего времени в размере не более 360 чел.-рейсов. Требуется определить количество рейсов для обоих типов самолетов, которые компания может выполнить, учитывая ограничения на количество пассажиров и размер фонда рабочего времени.

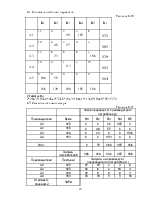
Таблица 1.1

1.2 Математическая модель.

Пусть: х - кол-во рейсов 1 типа х- кол-во рейсов 2 типа

Составим систему уравнений:

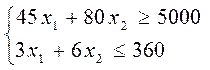
1.3 Решение на компьютере.

Таблица 1.2

1.4 Интерпретация результатов.

При заданных ограничениях кол-во рейсов 1 типа самолета – 40,  кол-во рейсов 2 типа самолета – 40.

2. Графоаналитический метод решения простейших оптимизационных моделей

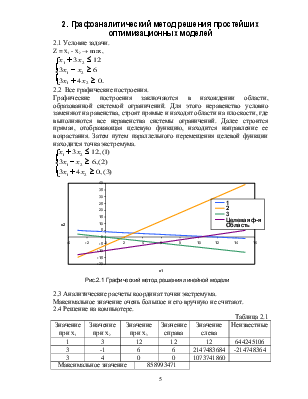
2.1 Условие задачи.

Z = х- х max,

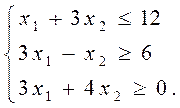
2.2  Все графические построения.

Графические построения заключаются в нахождении области, образованной системой ограничений. Для этого неравенство условно заменяют на равенства, строят прямые и находят области на плоскости, где выполняются все неравенства системы ограничений. Далее строится прямая, отображающая целевую функцию, находится направление ее возрастания. Затем путем параллельного перемещения целевой функции находится точка экстремума.

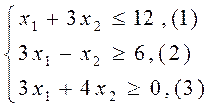
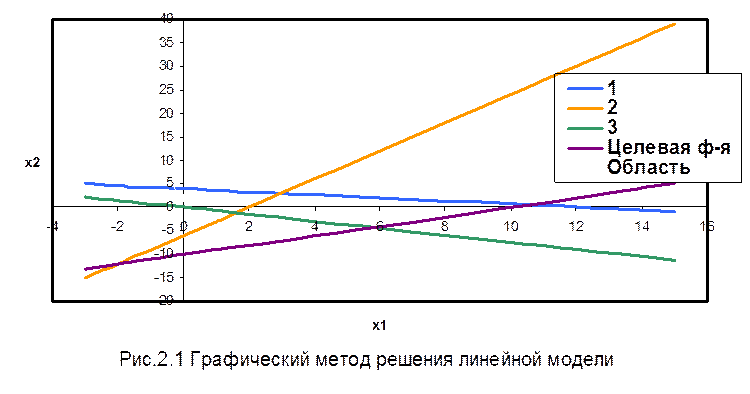2.3 Аналитические расчеты координат точки экстремума.

Максимальное значение очень большое и его вручную не считают.

2.4 Решение на компьютере.

Таблица 2.1

3. Симплексный метод решения линейных математических моделей

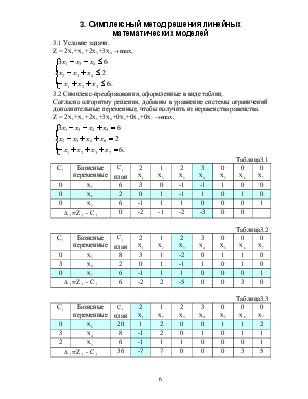
3.1 Условие задачи.

Z = 2х+х+2х+3хmax,

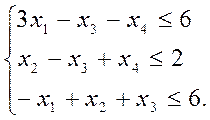
3.2 Симплекс-преобразования, оформленные в виде таблиц.

Согласно алгоритму решения, добавим в уравнение системы ограничений дополнительные переменные, чтобы получить из неравенства равенства.

Z = 2х+х+2х+3х+0х+0х+0хmax,

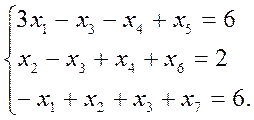
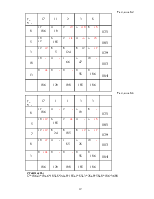
Таблица3.1

Таблица3.2

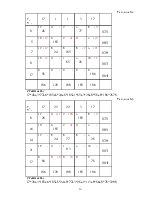
Таблица3.3

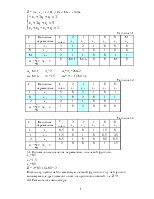
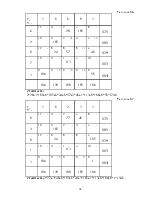
Таблица3.4

3.3 Оптимальные значения переменных и целевой функции.

х=20

х=0             х=26          х=28        

Z = 2*20+1*0+2*26+3*28=176

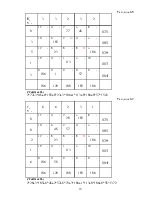
3.4 Решение на компьютере.

Таблица 3.5

4. Симплексный метод с искусственным базисом

4.1 Условие задачи.

Z = 2х+х-хmax,

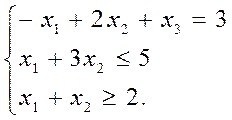
4.2 Симплекс-преобразования, оформленные в виде таблиц.

Согласно алгоритму решения, добавим в уравнение системы ограничений дополнительные переменные, чтобы получить из неравенства равенства