На шахте имеются три погрузочные машины и четыре забоя выработок, в каждом из которых одновременно может работать только одна машина. Сменная производительность машин в каждом забое приведена в таблице. Составить план расстановки машин по забоям. Необходимая производительность машин в забоях равна соответственно: в первом – 12, во втором – 9, в третьем – 11 и в четвертом – 13.
|
Машина |
Сменная производительность машин в забоях, м3 |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
9 |
5 |
8 |
12 |
|
2 |
8 |
6 |
7 |
9 |
|
3 |
8 |
7 |
7 |
8 |
В качестве переменных рекомендуется выбрать количество машин определенного типа, закрепленных за каждым забоем. Поскольку в забое может работать только одна машина, следовательно, эти переменные могут принимать только два значения – 0 или 1.
x1 – количество машин в первом забое;
x2– количество машин в втором забое;
x3– количество машин в третьем забое;
x4– количество машин в четвертом забое.
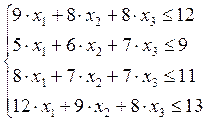
Решение системы на компьютере
|
Машина |
Сменная производительность машин в забое, м3 |
|||||
|
1 |
2 |
3 |
4 |
|||
|
1 |
9 |
5 |
8 |
12 |
X1 |
1 |
|
2 |
8 |
6 |
7 |
9 |
X2 |
0 |
|
3 |
8 |
7 |
7 |
8 |
X3 |
0 |
|
12 |
9 |
11 |
13 |
|||
|
9 |
5 |
8 |
12 |
|||
Из решения видно, что при постановке первой погрузочной машины в каждом из забоев, суммарная производительность всех забое максимальна.
|
Microsoft Excel 10.0 Отчет по результатам |
||||||
|
Рабочий лист: [Вариант 18.xls]Задача 1 |
||||||
|
Отчет создан: 09.06.2002 23:31:18 |
||||||
|
Целевая ячейка (Максимум) |
||||||
|
НЕТ |
||||||
|
Изменяемые ячейки |
||||||
|
Ячейка |
Имя |
Исходное значение |
Результат |
|||
|
$G$3 |
X1 |
0 |
1 |
|||
|
$G$4 |
X2 |
0 |
0 |
|||
|
$G$5 |
X3 |
0 |
0 |
|||
|
Ограничения |
||||||
|
Ячейка |
Имя |
Значение |
Формула |
Статус |
Разница |
|
|
$D$8 |
8 |
$D$8<=$D$6 |
не связан. |
3 |
||
|
$E$8 |
12 |
$E$8<=$E$6 |
не связан. |
1 |
||
|
$B$8 |
Сменная производительность машин в забое, м3 |
9 |
$B$8<=$B$6 |
не связан. |
3 |
|
|
$C$8 |
5 |
$C$8<=$C$6 |
не связан. |
4 |
||
|
$G$3 |
X1 |
1 |
$G$3=двоичное |
связанное |
0 |
|
|
$G$4 |
X2 |
0 |
$G$4=двоичное |
связанное |
0 |
|
|
$G$5 |
X3 |
0 |
$G$5=двоичное |
связанное |
0 |
|
![]()
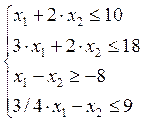
x1+2·x2=10 3·x1+2·x2=18 x1–x2=–8 ¾·x1–x2=9
x1=0 x2=5 x1=0 x2=9 x1=0 x2=8 x1=0 x2=–9
x1=4 x2=3 x1=2 x2=6 x1=–8 x2=0 x1=8 x2=–3
0=x1–4∙x2
x1=0 x2=0
x1=4 x2=1
![]()
|
Сi |
Базисные переменные |
Сj |
1 |
-1 |
1 |
0 |
0 |
|
план |
X1 |
X2 |
X3 |
X4 |
X5 |
||
|
0 |
X4 |
10 |
10 |
0 |
1 |
1 |
0 |
|
0 |
X5 |
10 |
0 |
10 |
1 |
0 |
1 |
|
Z(X0)=0 |
−1 |
1 |
–1 |
0 |
0 |
X0=(0;0;0;10;10)
Z(X0)=0
|
Сi |
Базисные переменные |
Сj |
1 |
-1 |
1 |
0 |
0 |
|
план |
X1 |
X2 |
X3 |
X4 |
X5 |
||
|
1 |
X3 |
10 |
10 |
0 |
1 |
1 |
0 |
|
0 |
X5 |
0 |
–10 |
10 |
0 |
–1 |
1 |
|
Z(X1)=10 |
9 |
1 |
0 |
1 |
0 |
X1=(0;0;10;0;0) – оптимальные значения переменных
Z(X0)=10 – Zmax оптимальное значение целевой функции
Решение математической модели на компьютере
|
Z |
10 |
Пр. часть |
Лев. Часть |
|
X1 |
0 |
10 |
10 |
|
X2 |
0 |
10 |
10 |
|
X3 |
10 |
|
Microsoft Excel 10.0 Отчет по результатам |
||||||
|
Рабочий лист: [Вариант 18.xls]Задача 3 |
||||||
|
Отчет создан: 10.06.2002 0:24:52 |
||||||
|
Целевая ячейка (Максимум) |
||||||
|
Ячейка |
Имя |
Исходное значение |
Результат |
|||
|
$B$1 |
Z |
0 |
10 |
|||
|
Изменяемые ячейки |
||||||
|
Ячейка |
Имя |
Исходное значение |
Результат |
|||
|
$B$2 |
X1 |
0 |
0 |
|||
|
$B$3 |
X2 |
0 |
0 |
|||
|
$B$4 |
X3 |
0 |
10 |
|||
|
Ограничения |
||||||
|
Ячейка |
Имя |
Значение |
Формула |
Статус |
Разница |
|
|
$B$6 |
Лев. Часть |
10 |
$B$6<=$A$6 |
связанное |
0 |
|
|
$B$7 |
Лев. Часть |
10 |
$B$7<=$A$7 |
связанное |
0 |
|
|
$B$2 |
X1 |
0 |
$B$2>=0 |
связанное |
0 |
|
|
$B$3 |
X2 |
0 |
$B$3>=0 |
связанное |
0 |
|
|
$B$4 |
X3 |
10 |
$B$4>=0 |
не связан. |
10 |
|
![]()
![]()
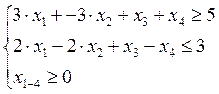
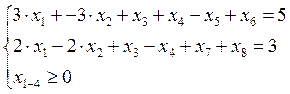
x6, x8 – искусственный базис.
|
Сi |
Базисные переменные |
Сj |
5 |
-5 |
1 |
1 |
0 |
М |
0 |
М |
|
план |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
||
|
М |
X6 |
5 |
3 |
-3 |
1 |
1 |
-1 |
1 |
0 |
0 |
|
М |
X8 |
3 |
2 |
-2 |
1 |
-1 |
0 |
0 |
1 |
1 |
|
Z(X0)=0 |
5М−5 |
−5М+5 |
2М-1 |
1 |
−М |
0 |
М |
0 |
|
Сi |
Базисные переменные |
Сj |
5 |
-5 |
1 |
1 |
0 |
0 |
М |
|
план |
X1 |
X2 |
X3 |
X4 |
X5 |
X7 |
X8 |
||
|
5 |
X1 |
5/3 |
1 |
-1 |
1/3 |
1/3 |
-1/3 |
0 |
0 |
|
М |
X8 |
-1/3 |
0 |
0 |
1/3 |
-5/3 |
2/3 |
1 |
1 |
|
Z(X1)=25/3 |
0 |
-10 |
М/3-2/3 |
-5М/3-2/3 |
2М/3-5/3 |
М |
0 |
|
Сi |
Базисные переменные |
Сj |
5 |
-5 |
1 |
1 |
0 |
0 |
|
план |
X1 |
X2 |
X3 |
X4 |
X5 |
X7 |
||
|
5 |
X1 |
5/3 |
1 |
-1 |
1/3 |
1/3 |
-1/3 |
0 |
|
0 |
X7 |
-1/3 |
0 |
0 |
1/3 |
-5/3 |
2/3 |
1 |
|
Z(X2)=25/3 |
0 |
0 |
2/3 |
2/3 |
-5/3 |
0 |
|
Сi |
Базисные переменные |
Сj |
5 |
-5 |
1 |
1 |
0 |
0 |
|
план |
X1 |
X2 |
X3 |
X4 |
X5 |
X7 |
||
|
1 |
X3 |
5 |
3 |
-3 |
1 |
1 |
-1 |
0 |
|
0 |
X7 |
-2 |
-1 |
1 |
0 |
-2 |
1 |
1 |
|
Z(X3)=5 |
-2 |
0 |
0 |
0 |
-1 |
0 |
|
Сi |
Базисные переменные |
Сj |
5 |
-5 |
1 |
1 |
0 |
0 |
|
план |
X1 |
X2 |
X3 |
X4 |
X5 |
X7 |
||
|
1 |
X3 |
-1 |
0 |
0 |
1 |
-5 |
2 |
3 |
|
-5 |
X2 |
-2 |
-1 |
1 |
0 |
-2 |
1 |
1 |
|
-2 |
0 |
0 |
0 |
-1 |
0 |
Решения математической модели нет, так как нет положительных коэффициентов в столбце.
Результат решения математической модели на компьютере
|
Z |
-1,1E+08 |
Лев. Ч. |
Прав. Ч. |
|
X1 |
0 |
5 |
5 |
|
X2 |
53687091 |
3 |
3 |
|
X3 |
1,34E+08 |
||
|
X4 |
26843547 |
На шахте имеются три погрузочные машины и четыре забоя выработок, в каждом из которых одновременно может работать только одна машина. Сменная производительность машин в каждом забое приведена в таблице. Составить план расстановки машин по забоям. Необходимая производительность машин в забоях равна соответственно: в первом – 12, во втором – 9, в третьем – 11 и в четвертом – 13.
|
Машина |
Сменная производительность машин в забоях, м3 |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
9 |
5 |
8 |
12 |
|
2 |
8 |
6 |
7 |
9 |
|
3 |
8 |
7 |
7 |
8 |
В качестве переменных рекомендуется выбрать количество машин определенного типа, закрепленных за каждым забоем. Поскольку в забое может работать только одна машина, следовательно, эти переменные могут принимать только два значения – 0 или 1.
Составить оптимальный план расстановки машин по забоям, чтобы достичь максимальной производительности всех машин.
![]() – целевая функция, равна сумме производительностей
всех машин в каждом забое
– целевая функция, равна сумме производительностей
всех машин в каждом забое
x1 – количество машин в первом забое;
x2– количество машин в втором забое;
x3– количество машин в третьем забое;
x4– количество машин в четвертом забое.
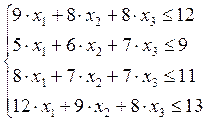
Результат решения математической модели на компьютере
|
Машина |
Сменная производительность машин в забое, м3 |
||||||
|
1 |
2 |
3 |
4 |
||||
|
1 |
9 |
5 |
8 |
12 |
X1 |
1 |
34 |
|
2 |
8 |
6 |
7 |
9 |
X2 |
0 |
0 |
|
3 |
8 |
7 |
7 |
8 |
X3 |
0 |
0 |
|
12 |
9 |
11 |
13 |
Целевая |
34 |
||
|
9 |
5 |
8 |
12 |
||||
Оптимальные значения переменных
Х=(1;0;0) м3
Оптимальное значение целевой функции
Z(X)=(9+5+8+12)∙1=34 м3.
|
Microsoft Excel 10.0 Отчет по результатам |
||||||
|
Рабочий лист: [Вариант 18.xls]Задача 5 |
||||||
|
Отчет создан: 10.06.2002 1:29:55 |
||||||
|
Целевая ячейка (Максимум) |
||||||
|
Ячейка |
Имя |
Исходное значение |
Результат |
|||
|
$H$6 |
0 |
34 |
||||
|
Изменяемые ячейки |
||||||
|
Ячейка |
Имя |
Исходное значение |
Результат |
|||
|
$G$3 |
X1 |
0 |
1 |
|||
|
$G$4 |
X2 |
0 |
0 |
|||
|
$G$5 |
X3 |
0 |
0 |
|||
|
Ограничения |
||||||
|
Ячейка |
Имя |
Значение |
Формула |
Статус |
Разница |
|
|
$D$8 |
8 |
$D$8<=$D$6 |
не связан. |
3 |
||
|
$E$8 |
12 |
$E$8<=$E$6 |
не связан. |
1 |
||
|
$B$8 |
Сменная производительность машин в забое, м3 |
9 |
$B$8<=$B$6 |
не связан. |
3 |
|
|
$C$8 |
5 |
$C$8<=$C$6 |
не связан. |
4 |
||
|
$G$3 |
X1 |
1 |
$G$3=двоичное |
связанное |
0 |
|
|
$G$4 |
X2 |
0 |
$G$4=двоичное |
связанное |
0 |
|
|
$G$5 |
X3 |
0 |
$G$5=двоичное |
связанное |
0 |
|
Ai=108; 93; 122; 136
Bj=138; 111; 109; 112; 122
|
15 |
22 |
19 |
25 |
9 |
|
16 |
12 |
21 |
18 |
18 |
|
20 |
24 |
13 |
27 |
8 |
|
4 |
19 |
15 |
19 |
11 |
Cij=
![]() , поэтому нужно
ввести фиктивного поставщика. При составлении модели объем производства
фиктивного поставщика принимается равным недостающему объему поставок, а
затраты на перевозки – равными нулю.
, поэтому нужно
ввести фиктивного поставщика. При составлении модели объем производства
фиктивного поставщика принимается равным недостающему объему поставок, а
затраты на перевозки – равными нулю.
|
Запросы потребителей |
В1 |
В2 |
В3 |
В4 |
В5 |
|
|
Производители: |
Поставки |
138 |
111 |
109 |
112 |
122 |
|
A1 |
108 |
15 |
22 |
19 |
25 |
18 |
|
A2 |
93 |
16 |
12 |
21 |
18 |
18 |
|
A3 |
122 |
20 |
24 |
13 |
27 |
8 |
|
A4 |
136 |
4 |
19 |
15 |
19 |
11 |
|
A5 – фикт. пост. |
133 |
0 |
0 |
0 |
0 |
0 |
Начальный план перевозок, заполненный методом северо–западного угла
|
28 |
24 |
13 |
17 |
17 |
Запасы |
|||||||
|
13 |
15 |
22 |
19 |
25 |
9 |
108 |
||||||
|
108 |
||||||||||||
|
12 |
16 |
12 |
21 |
18 |
18 |
93 |
||||||
|
30 |
63 |
|||||||||||
|
0 |
20 |
24 |
13 |
27 |
8 |
122 |
||||||
|
48 |
74 |
|||||||||||
|
-2 |
4 |
19 |
15 |
19 |
11 |
136 |
||||||
|
35 |
101 |
|||||||||||
|
17 |
0 |
0 |
0 |
0 |
0 |
133 |
||||||
|
11 |
122 |
|||||||||||
|
Потребности |
138 |
111 |
109 |
112 |
122 |
|||||||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
F=15·108+16·30+12·63+24·48+13·74+35·15+101∙19=7414
|
2 |
24 |
13 |
17 |
17 |
Запасы |
|||||||
|
-13 |
15 |
22 |
19 |
25 |
9 |
108 |
||||||
|
108 |
||||||||||||
|
12 |
16 |
12 |
21 |
18 |
18 |
93 |
||||||
|
93 |
||||||||||||
|
0 |
20 |
24 |
13 |
27 |
8 |
122 |
||||||
|
18 |
104 |
|||||||||||
|
-2 |
4 |
19 |
15 |
19 |
11 |
136 |
||||||
|
30 |
5 |
101 |
||||||||||
|
17 |
0 |
0 |
0 |
0 |
0 |
133 |
||||||
|
11 |
122 |
|||||||||||
|
Потребности |
138 |
111 |
109 |
112 |
122 |
|||||||
F=108·15+93·12+18·24+104·103+30·4+5·15+101·19=6634
|
17 |
24 |
13 |
32 |
32 |
Запасы |
|||||||
|
2 |
15 |
22 |
19 |
25 |
9 |
108 |
||||||
|
103 |
5 |
|||||||||||
|
12 |
16 |
12 |
21 |
18 |
18 |
93 |
||||||
|
93 |
||||||||||||
|
0 |
20 |
24 |
13 |
27 |
8 |
122 |
||||||
|
13 |
109 |
|||||||||||
|
13 |
4 |
19 |
15 |
19 |
11 |
136 |
||||||
|
35 |
5 |
101 |
||||||||||
|
17 |
0 |
0 |
0 |
0 |
0 |
133 |
||||||
|
11 |
122 |
|||||||||||
|
Потребности |
138 |
111 |
109 |
112 |
122 |
|||||||
F=103·15+5·22+93·12+13·24+109·13+35·4+5·15+101·19=6559
|
15 |
22 |
35 |
30 |
30 |
Запасы |
|||||||
|
0 |
15 |
22 |
19 |
25 |
9 |
108 |
||||||
|
90 |
18 |
|||||||||||
|
10 |
16 |
12 |
21 |
18 |
18 |
93 |
||||||
|
93 |
||||||||||||
|
1 |
20 |
24 |
13 |
27 |
8 |
122 |
||||||
|
109 |
13 |
|||||||||||
|
11 |
4 |
19 |
15 |
19 |
11 |
136 |
||||||
|
48 |
88 |
|||||||||||
|
17 |
0 |
0 |
0 |
0 |
0 |
133 |
||||||
|
24 |
109 |
|||||||||||
|
Потребности |
138 |
111 |
109 |
112 |
122 |
|||||||
F=90·15+18·22+93·12+109·13+13∙8+48·4+88·19=6247
|
15 |
22 |
14 |
9 |
9 |
Запасы |
|||||||
|
0 |
15 |
22 |
19 |
25 |
9 |
108 |
||||||
|
2 |
18 |
88 |
||||||||||
|
10 |
16 |
12 |
21 |
18 |
18 |
93 |
||||||
|
93 |
||||||||||||
|
1 |
20 |
24 |
13 |
27 |
8 |
122 |
||||||
|
109 |
13 |
|||||||||||
|
11 |
4 |
19 |
15 |
19 |
11 |
136 |
||||||
|
136 |
||||||||||||
|
9 |
0 |
0 |
0 |
0 |
0 |
133 |
||||||
|
112 |
21 |
|||||||||||
|
Потребности |
138 |
111 |
109 |
112 |
122 |
|||||||
F=2·15+18·22+88·9+93·12+109·13+13·8+136·4=4399
|
15 |
9 |
14 |
9 |
9 |
Запасы |
|||||||
|
0 |
15 |
22 |
19 |
25 |
9 |
108 |
||||||
|
2 |
106 |
|||||||||||
|
3 |
16 |
12 |
21 |
18 |
18 |
93 |
||||||
|
93 |
||||||||||||
|
1 |
20 |
24 |
13 |
27 |
8 |
122 |
||||||
|
109 |
13 |
|||||||||||
|
11 |
4 |
19 |
15 |
19 |
11 |
136 |
||||||
|
136 |
||||||||||||
|
9 |
0 |
0 |
0 |
0 |
0 |
133 |
||||||
|
18 |
112 |
3 |
||||||||||
|
Потребности |
138 |
111 |
109 |
112 |
122 |
|||||||
F=2·15+106·9+93·12+109·13+13·8+136·4=4165
|
8 |
8 |
13 |
8 |
8 |
Запасы |
|||||||
|
-1 |
15 |
22 |
19 |
25 |
9 |
108 |
||||||
|
108 |
||||||||||||
|
-4 |
16 |
12 |
21 |
18 |
18 |
93 |
||||||
|
93 |
||||||||||||
|
0 |
20 |
24 |
13 |
27 |
8 |
122 |
||||||
|
109 |
13 |
|||||||||||
|
9 |
4 |
19 |
15 |
19 |
11 |
136 |
||||||
|
136 |
||||||||||||
|
13 |
0 |
0 |
0 |
0 |
0 |
133 |
||||||
|
2 |
18 |
112 |
1 |
|||||||||
|
Потребности |
138 |
111 |
109 |
112 |
122 |
|||||||
F=108·9+93·12+109·13+13·8+136·4=4153
Оптимальный план перевозок
|
8 |
8 |
13 |
8 |
8 |
Запасы |
|||||||
|
-1 |
15 |
22 |
19 |
25 |
9 |
108 |
||||||
|
108 |
||||||||||||
|
-4 |
16 |
12 |
21 |
18 |
18 |
93 |
||||||
|
93 |
||||||||||||
|
0 |
20 |
24 |
13 |
27 |
8 |
122 |
||||||
|
108 |
14 |
|||||||||||
|
9 |
4 |
19 |
15 |
19 |
11 |
136 |
||||||
|
136 |
||||||||||||
|
13 |
0 |
0 |
0 |
0 |
0 |
133 |
||||||
|
2 |
18 |
1 |
112 |
|||||||||
|
Потребности |
138 |
111 |
109 |
112 |
122 |
|||||||
F=108·9+93·12+108·13+14·8+136·4=4148 – стоимость перевозок по оптимальному плану.
Результат решения на компьютере
|
Число перевозок от производителя i потребителю j |
||||||
|
Производители |
Всего |
B1 |
B2 |
B3 |
B4 |
B5 |
|
A1 |
108 |
0 |
0 |
0 |
0 |
108 |
|
A2 |
93 |
0 |
93 |
0 |
0 |
0 |
|
A3 |
122 |
0 |
0 |
108 |
0 |
14 |
|
A4 |
136 |
136 |
0 |
0 |
0 |
0 |
|
A5 |
133 |
2 |
18 |
1 |
112 |
0 |
|
Итого |
138 |
111 |
109 |
112 |
122 |
|
|
Запросы потребителей |
138 |
111 |
109 |
112 |
122 |
|
|
Производители: |
Поставки |
Затраты на перевозку от поставщика к потребителю |
||||
|
A1 |
108 |
15 |
22 |
19 |
25 |
9 |
|
A2 |
93 |
16 |
12 |
21 |
18 |
18 |
|
A3 |
122 |
20 |
24 |
13 |
27 |
8 |
|
A4 |
136 |
4 |
19 |
15 |
19 |
11 |
|
A5 |
133 |
0 |
0 |
0 |
0 |
0 |
|
4148 |
544 |
1116 |
1404 |
0 |
1084 |
|
|
Microsoft Excel 10.0 Отчет по результатам |
||||||
|
Рабочий лист: [Вариант 18.xls]Задача 6 |
||||||
|
Отчет создан: 10.06.2002 2:15:08 |
||||||
|
Целевая ячейка (Минимум) |
||||||
|
Ячейка |
Имя |
Исходное значение |
Результат |
|||
|
$B$18 |
Перевозка Поставки |
7414 |
4148 |
|||
|
Изменяемые ячейки |
||||||
|
Ячейка |
Имя |
Исходное значение |
Результат |
|||
|
$C$3 |
A1 B1 |
108 |
0 |
|||
|
$D$3 |
A1 B2 |
0 |
0 |
|||
|
$E$3 |
A1 B3 |
0 |
0 |
|||
|
$F$3 |
A1 B4 |
0 |
0 |
|||
|
$G$3 |
A1 B5 |
0 |
108 |
|||
|
$C$4 |
A2 B1 |
30 |
0 |
|||
|
$D$4 |
A2 B2 |
63 |
93 |
|||
|
$E$4 |
A2 B3 |
0 |
0 |
|||
|
$F$4 |
A2 B4 |
0 |
0 |
|||
|
$G$4 |
A2 B5 |
0 |
0 |
|||
|
$C$5 |
A3 B1 |
0 |
0 |
|||
|
$D$5 |
A3 B2 |
48 |
0 |
|||
|
$E$5 |
A3 B3 |
74 |
108 |
|||
|
$F$5 |
A3 B4 |
0 |
0 |
|||
|
$G$5 |
A3 B5 |
0 |
14 |
|||
|
$C$6 |
A4 B1 |
0 |
136 |
|||
|
$D$6 |
A4 B2 |
0 |
0 |
|||
|
$E$6 |
A4 B3 |
35 |
0 |
|||
|
$F$6 |
A4 B4 |
101 |
0 |
|||
|
$G$6 |
A4 B5 |
0 |
0 |
|||
|
$C$7 |
A5 B1 |
0 |
2 |
|||
|
$D$7 |
A5 B2 |
0 |
18 |
|||
|
$E$7 |
A5 B3 |
0 |
1 |
|||
|
$F$7 |
A5 B4 |
11 |
112 |
|||
|
$G$7 |
A5 B5 |
122 |
0 |
|||
|
Ограничения |
||||||
|
Ячейка |
Имя |
Значение |
Формула |
Статус |
Разница |
|
|
$B$3 |
A1 Всего: |
108 |
$B$3=$B$12 |
не связан. |
0 |
|
|
$C$9 |
B1 |
138 |
$C$9=$C$10 |
не связан. |
0 |
|
|
$E$9 |
B3 |
109 |
$E$9=$E$10 |
не связан. |
0 |
|
|
$F$9 |
B4 |
112 |
$F$9=$F$10 |
не связан. |
0 |
|
|
$G$9 |
B5 |
122 |
$G$9=$G$10 |
не связан. |
0 |
|
|
$B$4 |
A2 Всего: |
93 |
$B$4=$B$13 |
не связан. |
0 |
|
|
$B$5 |
A3 Всего: |
122 |
$B$5=$B$14 |
не связан. |
0 |
|
|
$B$6 |
A4 Всего: |
136 |
$B$6=$B$15 |
не связан. |
0 |
|
|
$B$7 |
A5 Всего: |
133 |
$B$7=$B$16 |
не связан. |
0 |
|
|
$D$9 |
B2 |
111 |
$D$9=$D$10 |
не связан. |
0 |
|
|
$C$3 |
A1 B1 |
0 |
$C$3=целое |
связанное |
0 |
|
|
$D$3 |
A1 B2 |
0 |
$D$3=целое |
связанное |
0 |
|
|
$E$3 |
A1 B3 |
0 |
$E$3=целое |
связанное |
0 |
|
|
$F$3 |
A1 B4 |
0 |
$F$3=целое |
связанное |
0 |
|
|
$G$3 |
A1 B5 |
108 |
$G$3=целое |
связанное |
0 |
|
|
$C$4 |
A2 B1 |
0 |
$C$4=целое |
связанное |
0 |
|
|
$D$4 |
A2 B2 |
93 |
$D$4=целое |
связанное |
0 |
|
|
$E$4 |
A2 B3 |
0 |
$E$4=целое |
связанное |
0 |
|
|
$F$4 |
A2 B4 |
0 |
$F$4=целое |
связанное |
0 |
|
|
$G$4 |
A2 B5 |
0 |
$G$4=целое |
связанное |
0 |
|
|
$C$5 |
A3 B1 |
0 |
$C$5=целое |
связанное |
0 |
|
|
$D$5 |
A3 B2 |
0 |
$D$5=целое |
связанное |
0 |
|
|
$E$5 |
A3 B3 |
108 |
$E$5=целое |
связанное |
0 |
|
|
$F$5 |
A3 B4 |
0 |
$F$5=целое |
связанное |
0 |
|
|
$G$5 |
A3 B5 |
14 |
$G$5=целое |
связанное |
0 |
|
|
$C$6 |
A4 B1 |
136 |
$C$6=целое |
связанное |
0 |
|
|
$D$6 |
A4 B2 |
0 |
$D$6=целое |
связанное |
0 |
|
|
$E$6 |
A4 B3 |
0 |
$E$6=целое |
связанное |
0 |
|
|
$F$6 |
A4 B4 |
0 |
$F$6=целое |
связанное |
0 |
|
|
$G$6 |
A4 B5 |
0 |
$G$6=целое |
связанное |
0 |
|
|
$C$7 |
A5 B1 |
2 |
$C$7=целое |
связанное |
0 |
|
|
$D$7 |
A5 B2 |
18 |
$D$7=целое |
связанное |
0 |
|
|
$E$7 |
A5 B3 |
1 |
$E$7=целое |
связанное |
0 |
|
|
$F$7 |
A5 B4 |
112 |
$F$7=целое |
связанное |
0 |
|
|
$G$7 |
A5 B5 |
0 |
$G$7=целое |
связанное |
0 |
|
Задача 7. Поиск кратчайших расстояний на транспортной сети
Вершины транспортной сети: Павлоград, Чаплино, Камыш-Заря, Федоровка, Энергоград, Запорожье, Апостолово, Моисеевка, Пятихатки, Красноград.
Начальная вершина: Нововеселая.
Схема транспортной сети
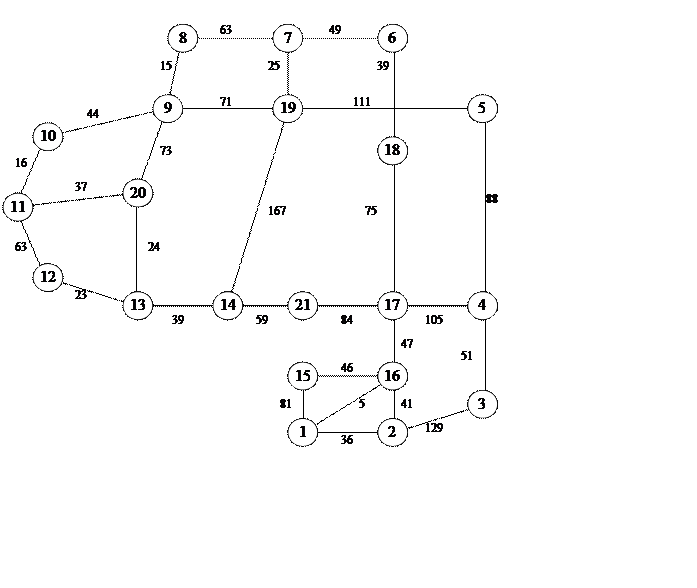
|
Номер вершины |
Название станции |
|
1 |
Нововеселая |
|
2 |
Федоровка |
|
3 |
Камыш-Заря |
|
4 |
Пологи |
|
5 |
Чаплино |
|
6 |
Павлоград |
|
7 |
Новомосковск |
|
8 |
Дзержинск |
|
9 |
Верховцево |
|
10 |
Пятихатки |
|
11 |
Савро |
|
12 |
Моисеевка |
|
13 |
Кривой-Рог |
|
14 |
Апосолово |
|
15 |
Энергоград |
|
16 |
Таврическ |
|
17 |
Запорожье |
|
18 |
Синельниково |
|
19 |
Днепропетровск |
|
20 |
Приворот |
|
21 |
Никополь |
Таблицы оптимальных путей
|
i |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
|
1 |
-1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
2 |
2 |
1000 |
-1 |
36 |
1 |
36 |
1 |
36 |
1 |
36 |
1 |
36 |
1 |
36 |
|
3 |
3 |
1000 |
3 |
1000 |
-2 |
165 |
2 |
165 |
2 |
165 |
2 |
165 |
2 |
165 |
|
4 |
4 |
1000 |
4 |
1000 |
4 |
1000 |
-3 |
216 |
-3 |
216 |
-17 |
157 |
17 |
157 |
|
5 |
5 |
1000 |
5 |
1000 |
5 |
1000 |
5 |
1000 |
5 |
1000 |
5 |
1000 |
-4 |
245 |
|
6 |
6 |
1000 |
6 |
1000 |
6 |
1000 |
6 |
1000 |
6 |
1000 |
6 |
1000 |
6 |
1000 |
|
7 |
7 |
1000 |
7 |
1000 |
7 |
1000 |
7 |
1000 |
7 |
1000 |
7 |
1000 |
7 |
1000 |
|
8 |
8 |
1000 |
8 |
1000 |
8 |
1000 |
8 |
1000 |
8 |
1000 |
8 |
1000 |
8 |
1000 |
|
9 |
9 |
1000 |
9 |
1000 |
9 |
1000 |
9 |
1000 |
9 |
1000 |
9 |
1000 |
9 |
1000 |
|
10 |
10 |
1000 |
10 |
1000 |
10 |
1000 |
10 |
1000 |
10 |
1000 |
10 |
1000 |
10 |
1000 |
|
11 |
11 |
1000 |
11 |
1000 |
11 |
1000 |
11 |
1000 |
11 |
1000 |
11 |
1000 |
11 |
1000 |
|
12 |
12 |
1000 |
12 |
1000 |
12 |
1000 |
12 |
1000 |
12 |
1000 |
12 |
1000 |
12 |
1000 |
|
13 |
13 |
1000 |
13 |
1000 |
13 |
1000 |
13 |
1000 |
13 |
1000 |
13 |
1000 |
13 |
1000 |
|
14 |
14 |
1000 |
14 |
1000 |
14 |
1000 |
14 |
1000 |
14 |
1000 |
14 |
1000 |
14 |
1000 |
|
15 |
15 |
1000 |
-1 |
81 |
-1 |
81 |
-1 |
81 |
-16 |
51 |
16 |
51 |
16 |
51 |
|
16 |
16 |
1000 |
-1 |
5 |
-1 |
5 |
-1 |
5 |
1 |
5 |
1 |
5 |
1 |
5 |
|
17 |
17 |
1000 |
17 |
1000 |
17 |
1000 |
17 |
1000 |
-16 |
52 |
16 |
52 |
16 |
52 |
|
18 |
18 |
1000 |
18 |
1000 |
18 |
1000 |
18 |
1000 |
18 |
1000 |
-17 |
127 |
-17 |
127 |
|
19 |
19 |
1000 |
19 |
1000 |
19 |
1000 |
19 |
1000 |
19 |
1000 |
19 |
1000 |
19 |
1000 |
|
20 |
20 |
1000 |
20 |
1000 |
20 |
1000 |
20 |
1000 |
20 |
1000 |
20 |
1000 |
20 |
1000 |
|
21 |
21 |
1000 |
21 |
1000 |
21 |
1000 |
21 |
1000 |
21 |
1000 |
-17 |
136 |
-17 |
136 |
|
i |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
2 |
1 |
36 |
1 |
36 |
1 |
36 |
1 |
36 |
1 |
36 |
1 |
36 |
1 |
36 |
|
3 |
2 |
165 |
2 |
165 |
2 |
165 |
2 |
165 |
2 |
165 |
2 |
165 |
2 |
165 |
|
4 |
17 |
157 |
17 |
157 |
17 |
157 |
17 |
157 |
17 |
157 |
17 |
157 |
17 |
157 |
|
5 |
-4 |
245 |
4 |
245 |
4 |
245 |
4 |
245 |
4 |
245 |
4 |
245 |
4 |
245 |
|
6 |
6 |
1000 |
6 |
1000 |
6 |
1000 |
6 |
1000 |
6 |
1000 |
6 |
1000 |
6 |
1000 |
|
7 |
7 |
1000 |
7 |
1000 |
7 |
1000 |
7 |
1000 |
7 |
1000 |
7 |
1000 |
7 |
1000 |
|
8 |
8 |
1000 |
8 |
1000 |
8 |
1000 |
8 |
1000 |
8 |
1000 |
8 |
1000 |
8 |
1000 |
|
9 |
9 |
1000 |
9 |
1000 |
9 |
1000 |
9 |
1000 |
9 |
1000 |
-20 |
331 |
-20 |
331 |
|
10 |
10 |
1000 |
10 |
1000 |
10 |
1000 |
10 |
1000 |
10 |
1000 |
10 |
1000 |
-11 |
311 |
|
11 |
11 |
1000 |
11 |
1000 |
11 |
1000 |
11 |
1000 |
-12 |
320 |
-20 |
295 |
20 |
295 |
|
12 |
12 |
1000 |
12 |
1000 |
12 |
1000 |
-13 |
257 |
13 |
257 |
13 |
257 |
13 |
257 |
|
13 |
13 |
1000 |
13 |
1000 |
-14 |
234 |
14 |
234 |
14 |
234 |
14 |
234 |
14 |
234 |
|
14 |
-21 |
195 |
-21 |
195 |
21 |
195 |
21 |
195 |
21 |
195 |
21 |
195 |
21 |
195 |
|
15 |
16 |
51 |
16 |
51 |
16 |
51 |
16 |
51 |
16 |
51 |
16 |
51 |
16 |
51 |
|
16 |
1 |
5 |
1 |
5 |
1 |
5 |
1 |
5 |
1 |
5 |
1 |
5 |
1 |
5 |
|
17 |
16 |
52 |
16 |
52 |
16 |
52 |
16 |
52 |
16 |
52 |
16 |
52 |
16 |
52 |
|
18 |
-17 |
127 |
-17 |
127 |
-17 |
127 |
-17 |
127 |
-17 |
127 |
-17 |
127 |
-17 |
127 |
|
19 |
19 |
1000 |
-5 |
356 |
-5 |
356 |
-5 |
356 |
-5 |
356 |
-5 |
356 |
-5 |
356 |
|
20 |
20 |
1000 |
20 |
1000 |
20 |
1000 |
-13 |
258 |
-13 |
258 |
13 |
258 |
13 |
258 |
|
21 |
17 |
136 |
17 |
136 |
17 |
136 |
17 |
136 |
17 |
136 |
17 |
136 |
17 |
136 |
|
i |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
li |
pi |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
2 |
1 |
36 |
1 |
36 |
1 |
36 |
1 |
36 |
1 |
36 |
1 |
36 |
1 |
36 |
|
3 |
2 |
165 |
2 |
165 |
2 |
165 |
2 |
165 |
2 |
165 |
2 |
165 |
2 |
165 |
|
4 |
17 |
157 |
17 |
157 |
17 |
157 |
17 |
157 |
17 |
157 |
17 |
157 |
17 |
157 |
|
5 |
4 |
245 |
4 |
245 |
4 |
245 |
4 |
245 |
4 |
245 |
4 |
245 |
4 |
245 |
|
6 |
6 |
1000 |
-18 |
166 |
18 |
166 |
18 |
166 |
18 |
166 |
18 |
166 |
18 |
166 |
|
7 |
7 |
1000 |
7 |
1000 |
-6 |
215 |
6 |
215 |
6 |
215 |
6 |
215 |
6 |
215 |
|
8 |
8 |
1000 |
8 |
1000 |
8 |
1000 |
-7 |
278 |
-7 |
278 |
7 |
278 |
7 |
278 |
|
9 |
-20 |
331 |
-20 |
331 |
-20 |
331 |
-20 |
331 |
-19 |
311 |
-8 |
293 |
8 |
293 |
|
10 |
11 |
311 |
11 |
311 |
11 |
311 |
11 |
311 |
11 |
311 |
11 |
311 |
11 |
311 |
|
11 |
20 |
295 |
20 |
295 |
20 |
295 |
20 |
295 |
20 |
295 |
20 |
295 |
20 |
295 |
|
12 |
13 |
257 |
13 |
257 |
13 |
257 |
13 |
257 |
13 |
257 |
13 |
257 |
13 |
257 |
|
13 |
14 |
234 |
14 |
234 |
14 |
234 |
14 |
234 |
14 |
234 |
14 |
234 |
14 |
234 |
|
14 |
21 |
195 |
21 |
195 |
21 |
195 |
21 |
195 |
21 |
195 |
21 |
195 |
21 |
195 |
|
15 |
16 |
51 |
16 |
51 |
16 |
51 |
16 |
51 |
16 |
51 |
16 |
51 |
16 |
51 |
|
16 |
1 |
5 |
1 |
5 |
1 |
5 |
1 |
5 |
1 |
5 |
1 |
5 |
1 |
5 |
|
17 |
16 |
52 |
16 |
52 |
16 |
52 |
16 |
52 |
16 |
52 |
16 |
52 |
16 |
52 |
|
18 |
-17 |
127 |
17 |
127 |
17 |
127 |
17 |
127 |
17 |
127 |
17 |
127 |
17 |
127 |
|
19 |
-5 |
356 |
-5 |
356 |
-5 |
356 |
-7 |
240 |
7 |
240 |
7 |
240 |
7 |
240 |
|
20 |
13 |
258 |
13 |
258 |
13 |
258 |
13 |
258 |
13 |
258 |
13 |
258 |
13 |
258 |
|
21 |
17 |
136 |
17 |
136 |
17 |
136 |
17 |
136 |
17 |
136 |
17 |
136 |
17 |
136 |
Конечные вершины транспортной сети: 3, 5, 9, 10, 12, 15, 19.
Оптимальные маршруты: [1–2–3] – 165
[1–16–15] – 51
[1–16–17–4–5] – 245
[1–16–17–18–6–7–19] – 240
[1–16–17–18–6–7–8–9] – 293
[1–16–17–21–14–13–12] – 257
[1–16–17–21–14–13–20–11–10] – 311
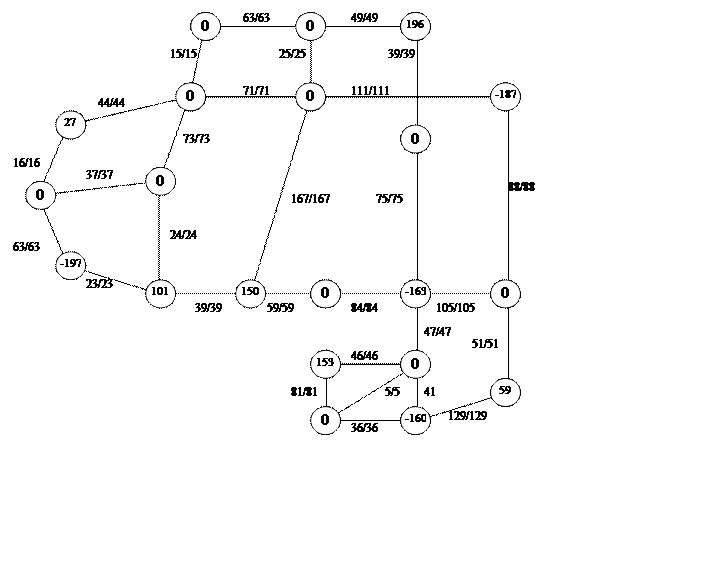
Задача 8. Решение транспортной задачи в сетевой постановке методом сокращения невязки
Объемы производства и потребления пиломатериалов для транспортной сети
|
Пиломатериалы |
|
|
Павлоград |
196 |
|
Чаплино |
-187 |
|
Камыш-Заря |
59 |
|
Федоровка |
-160 |
|
Энергоград |
153 |
|
Запорожье |
-163 |
|
Апостолово |
159 |
|
Моисеевка |
-197 |
|
Пятихатки |
27 |
|
Красноград |
101 |
|
i |
li |
pi |
|
1 |
16 |
51 |
|
2 |
16 |
87 |
|
3 |
3 |
0 |
|
4 |
3 |
51 |
|
5 |
4 |
139 |
|
6 |
6 |
0 |
|
7 |
6 |
49 |
|
8 |
9 |
59 |
|
9 |
10 |
44 |
|
10 |
10 |
0 |
|
11 |
10 |
16 |
|
12 |
13 |
23 |
|
13 |
13 |
0 |
|
14 |
14 |
0 |
|
15 |
15 |
0 |
|
16 |
15 |
46 |
|
17 |
16 |
93 |
|
18 |
6 |
39 |
|
19 |
7 |
74 |
|
20 |
13 |
24 |
|
21 |
14 |
59 |
Кратчайшие маршруты:
[15–16–2]
[15–16–17]
[13–12]
[3–4–5]
|
i |
li |
pi |
|
1 |
16 |
72 |
|
2 |
16 |
108 |
|
3 |
4 |
46 |
|
4 |
5 |
97 |
|
5 |
19 |
185 |
|
6 |
6 |
0 |
|
7 |
6 |
49 |
|
8 |
9 |
59 |
|
9 |
10 |
44 |
|
10 |
10 |
0 |
|
11 |
10 |
16 |
|
12 |
13 |
62 |
|
13 |
14 |
39 |
|
14 |
14 |
0 |
|
15 |
16 |
21 |
|
16 |
17 |
67 |
|
17 |
18 |
114 |
|
18 |
6 |
39 |
|
19 |
7 |
74 |
|
20 |
11 |
53 |
|
21 |
14 |
59 |
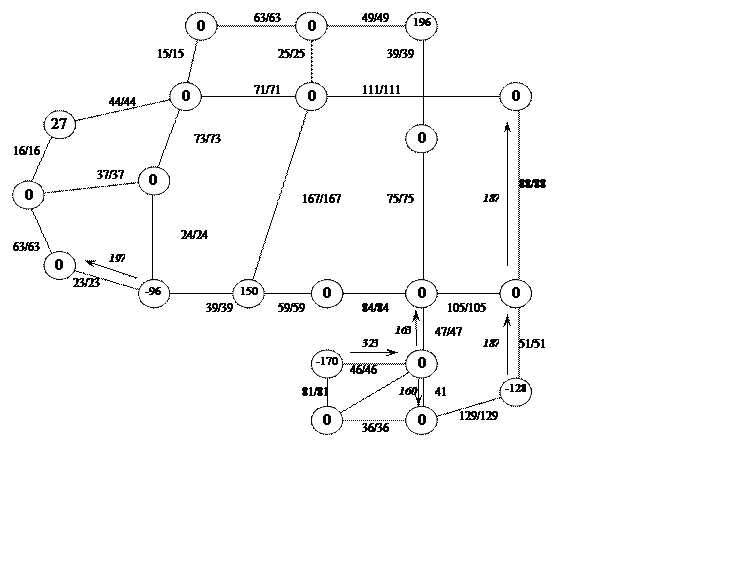
Кратчайшие маршруты:
[14–13]
[6–18–17–16–15]
[6–7–19–5–4–3]
|
i |
li |
pi |
|
1 |
16 |
195 |
|
2 |
3 |
183 |
|
3 |
4 |
75 |
|
4 |
5 |
126 |
|
5 |
19 |
214 |
|
6 |
18 |
29 |
|
7 |
6 |
78 |
|
8 |
9 |
59 |
|
9 |
10 |
44 |
|
10 |
10 |
0 |
|
11 |
10 |
16 |
|
12 |
13 |
62 |
|
13 |
14 |
39 |
|
14 |
14 |
0 |
|
15 |
16 |
144 |
|
16 |
17 |
190 |
|
17 |
21 |
143 |
|
18 |
17 |
68 |
|
19 |
7 |
103 |
|
20 |
11 |
53 |
|
21 |
14 |
59 |
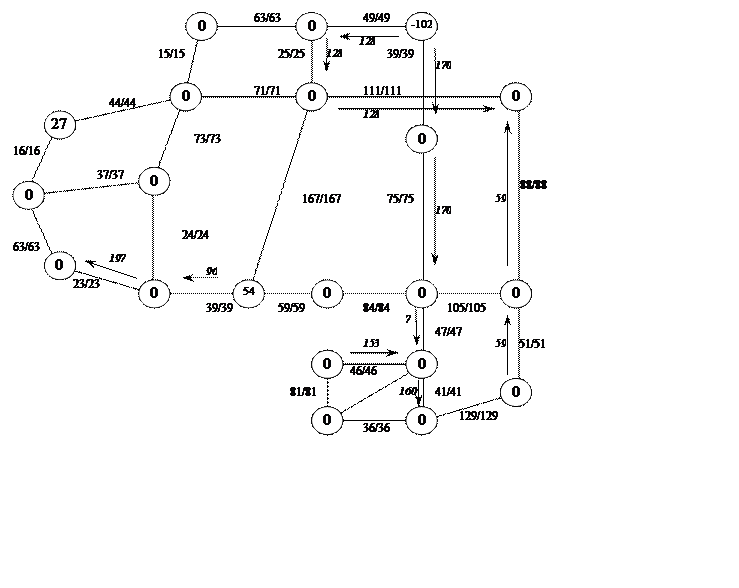
Кратчайшие маршруты:
[14–21–17–18–6]
|
i |
li |
pi |
|
1 |
16 |
159 |
|
2 |
3 |
195 |
|
3 |
4 |
87 |
|
4 |
5 |
138 |
|
5 |
19 |
226 |
|
6 |
7 |
41 |
|
7 |
19 |
90 |
|
8 |
9 |
59 |
|
9 |
10 |
44 |
|
10 |
10 |
0 |
|
11 |
10 |
16 |
|
12 |
13 |
26 |
|
13 |
14 |
3 |
|
14 |
21 |
-36 |
|
15 |
16 |
108 |
|
16 |
2 |
154 |
|
17 |
16 |
107 |
|
18 |
17 |
32 |
|
19 |
9 |
115 |
|
20 |
13 |
27 |
|
21 |
17 |
23 |
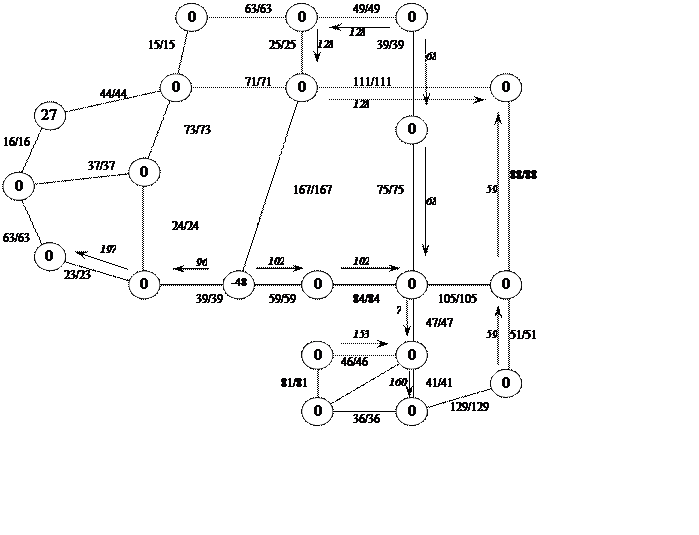
Кратчайшие маршруты:
[10–9–19–5–4–3–2–16–17–21–14]
Оптимальный план перевозок
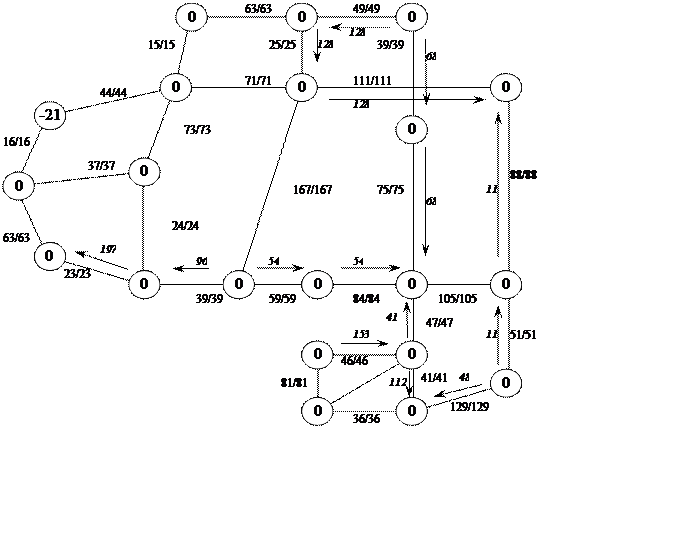
Затраты на транспортировку:
F=153·46+41·47+112·41+48·129+11·51+11·88+176·111+68·75+54·84+ +54·59+96·36+197·23+68·39+128·49+128·25+48·71+48·44=79555
Задача 9. Расчет оптимального варианта плана формирования поездов
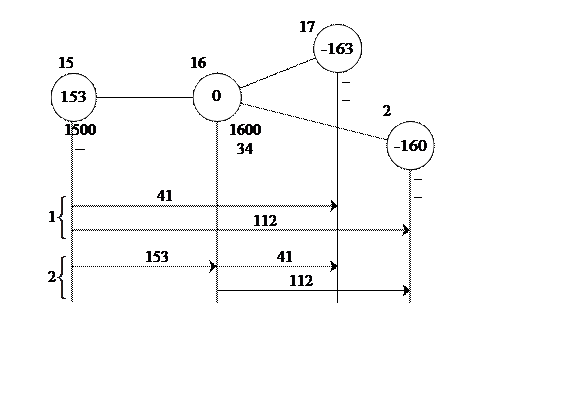

Затраты вагонно-часов на формирование и переработку поездов:
T1=2∙Cm15=3000 ваг. час.
T2=Cm15+2∙Cm16+N15,17∙T16+N15,2∙T16=1500+2∙1600+41∙34+112∙34=8302 ваг. час.
В первом варианте оба поезда формируются на станции 15 по отдельности и следуют до станций назначения без переработки на станции 16. Во втором случае, поезда объединяются в струю на участке 15–16, на станции 16 проходят
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.