Определение площади строительства складов двух типов при продолжительности работ в 200 дней при двухсменной работе

оптимальных значениях x₁=0, x₂=4, x₃=2, x₄=0, x₅=0, x₆=0 целевая функция Z(x) принимает максимальное значение: Z (max) = 10.

Результаты решения задачи с помощью макроса MS Excel «Поиск решение» представлены в таблице 3.4:

Таблица 3.4 – Результаты решения

Уравнения	Коэффициенты при переменных			Контроль ограничений	Ограничения
1	2	1	-1	2	2
2	2	-1	5	6	6
3	8	2	2	12	12
Коэф-ты целевой функции	1	2	1
	0	4	2	10

Вывод: решив задачу при помощи симплексных преобразований, мы пришли к оптимальному решению, т. е. когда в индексной строке отсутствуют отрицательные значения и это решение совпало с решением, полученным с помощью  макроса MC Excel «Поиск решение».

4. Решение задачи симплексным методом с искусственным базисом

Условие:

Z = x₁-2x₂-x₃ → max;

                               

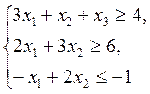
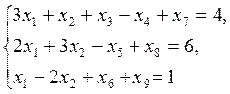
Z =- x₁+2x₂+x₃ +0x₄+0x₅+0x₆+Mx₇+Mx₈+Mx₉→ min;

где  - базисные переменные

 - искусственные базисные переменные.

Решение производим с помощью таблиц (4.1-4.5) симплексным методом:

Таблица 4.1 – Итерация№1

Ci	Базис	Cj	-1	+2	+1	0	0	0	M	M	M
		План	X1	X2	X3	X4	X5	X6	X7	X8	X9
M	X7	4	3	1	1	-1	0	0	1	0	0
M	X8	6	2	3	0	0	-1	0	0	1	0
M	X9	1	1	-2	0	0	0	+1	0	0	1
		11M	6M+1	2M-2	M-1	(-)M	(-)M	(-)M	0	0	0

                                 

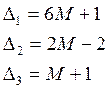
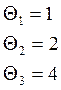
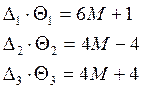
Таблица 4.2 – Итерация№2

Ci	Базис	Cj	-1	+2	+1	0	0	0	M	M
		План	X1	X2	X3	X4	X5	X6	X7	X8
M	X7	1	0	7	1	-1	0	-3	1	0
M	X8	4	0	7	0	0	-1	-2	0	1
-1	X1	1	1	-2	0	0	0	+1	0	0
		5M-1	0	14M	M-1	(-)M	(-)M	-5M-1	0	0

                                 

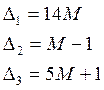
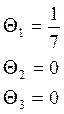
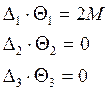
Таблица 4.3 – Итерация№3

Ci	Базис	Cj	-1	+2	+1	0	0	0	M
		План	X1	X2	X3	X4	X5	X6	X8
2	X2	1/7	0	1	1/7	- 1/7	0	-3/7	1/7
M	X8	3	0	0	-1	1	-1	1	-1
-1	X1	9/7	1	0	2/7	- 2/7	0	1/7	2/7
		3M-1	0	0	(-)M-1	M	(-)M	(-)M+1	(-)2M

                                 

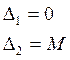
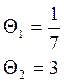
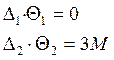
Таблица 4.4 – Итерация№4

Ci	Базис	Cj	-1	+2	+1	0	0	0
		План	X1	X2	X3	X4	X5	X6
2	X2	4/7	0	1	0	0	- 1/7	-2/7
0	X4	3	0	0	-1	1	-1	1
-1	X1	15/7	1	0	0	0	- 2/7	3/7
		-1	0	0	-1	0	0	-1

При оптимальных значениях x₁=15/7, x₂=4/7, x₃=0 целевая функция z(x) принимает максимальное значение.  Z (max) = 1.

Результаты решения задачи с помощью макроса MC Excel «Поиск решение» представлены в таблице 4.6:

Таблица 4.6 – Результаты решения

Уравнения	Коэффициенты при переменных			Контроль ограничений	Ограничения
1	3	1	1	4	4
2	2	3	0	6	6
3	-1	2	0	-1	-1
Коэффициент в целевой функции	1	-2	-1
	15/7	4/7	0	1

Вывод: при решении симплексным методом с искусственным базисом  получили оптимальное значение, которое соответствует отсутствию положительных значений в индексной строке и эти полученные значения совпадают с решением при помощи макроса MC Excel «Поиск решение».

5. Построение и решение линейных оптимизационных моделей

Используя уже готовую дескриптивную модель, содержащую переменные и ограничения модели, требуется сформулировать целевую функцию оптимизационной модели.

При проектировании участка комплексной механизации погрузочно-разгрузочных работ прокатного цеха были выбраны два варианта строительства склада, различных по конструктивным решениям. На строительстве используется два одинаковых экскаватора и десять одинаковых кранов. Известны затраты машино-смен на строительство 10 м²  склада (приведены в таблице). Требуется определить площадь строительства складов каждого типа, если продолжительность работ по проекту составляет 200 дней при двухсменной работе.

Определить площадь строительства складов каждого типа так, чтобы  суммарная площадь была максимальной.

Таблица 5.1 – Начальные условия

Тип склада	Затраты машино-смен на строительство 10 м2 склада
	экскаваторов	кранов
1	0,2	2
2	0,3	1

Пусть x₁ – площадь 1-го склада, x₂ – площадь 2-го склада.

Составим систему уравнений:

0,02 x₁ + 0,03 x₂ £ 800;

0,2 x₁ + 0,1 x₂ £ 4000.

Z= x₁+ x₂ → max;

Z – целевая функция, показывающая максимальную суммарную площадь складов.

Результаты решения представлены в таблице 5.2:

Таблица 5.2 – Результаты решения

Тип склада	Затраты машино-смен на строительство 1 м2		Кол-во экскаваторов	Кол-во кранов	Кол-во смен
	экскаваторов	кранов
1	0,02	0,2	2	10	400
2	0,03	0,1	2	10	400
	Площадь складов		Ограничения	Контроль ограничений	Плановые затраты машино-смен
	X1	X2
	20000	26667	1200	800	экскаваторов
			0	4000	кранов
	Суммарная площадь складов	46667

При оптимальных значений переменных x₁=20000 м² и x₂=26667 м² целевая функция z(x) достигает максимального значения и равна 46667 м²

Интерпретация полученных результатов:

Определили площадь 1-го склада равную 20000 м² и 2-го равную 26667м² при соответствующих затратах машино-смен и в итоге получили суммарную площадь обоих складов, которая соответствует максимуму.

Вывод: Поскольку система уравнений, описывающая условия дескриптивной модели, имеет дополнительные ограничения и содержит целевую функцию то найденные значения переменных, являются оптимальным решением данной системы.

6. Решение транспортной задачи линейного программирования в матричной постановке методом потенциалов

Требуется найти объемы поставок от каждого поставщика каждому потребителю, чтобы суммарные затраты на все перевозки были минимальными.

Условие:

A_i =137  122  103  105  100

B_j = 102  115  115  121  

Таблица 6.1 – Тарифы на перевозку

Cij=	16	4	20	6
	3	22	8	10
	19	9	21	13
	2	16	6	5
	3	2	11	8

Математическая модель:

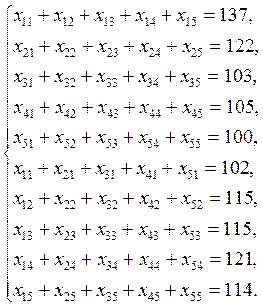
Целевая функция:

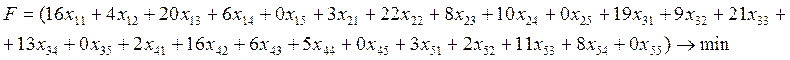
Определение типа задачи:

;

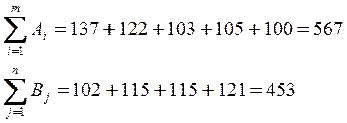
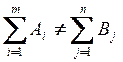Исходя из того, что продукция производится больше, чем потребляется, следовательно, задачу следует привести к закрытому типу, добавив фиктивного потребителя, как это показано на таблице 6:2.

Таблица 6.2 – Начальный план

	39		27		13		5		0
-23	16		4		20	30	6	24	0	23	137
	102		35
-5	3	-31	22		8		10	10	0	5	122
			80		42
8	19	-28	9	-26	21		13		0	-8	103
					73		30
0	2	-37	16	-11	6	-7	5		0		105
							91		14
0	3	-36	2	-25	11	-2	8	3	0		100
									100
	105		115		115		121		114

F_н(x)  = 16 * 102 + 4 * 35 + 22 * 80 + 8 * 42 + 21 * 73 + 13 * 30 + 5 * 91 + 0 * 14 + 0 * 100 = 6246

Следующий этап, представленный на таблицах 6.3-6.10, заключается в составлении такого плана перевозок, чтобы суммарные затраты на все перевозки были минимальны.

Таблица 6.3 – Цикл №1

	2		-10		-24		5		0
14	16		4		20	30	6	-13	0	-14	137
	29		108
32	3	-31	22		8		10	-27	0	-32	122
			7		115
8	19	9	9	11	21	37	13		0	-8	103
							103
0	2		16	26	6	30	5		0		105
	73						18		14
0	3	1	2	12	11	35	8	3	0		100
									100
	105		115		115		121		114

F(x) = 3545

Таблица 6.4 – Цикл №2

	16		4		-10		6		14
0	16		4		20	30	6		0	-14	137
	11		108				18
18	3	-31	22		8		10	-14	0	-32	122
			7		115
7	19	-4	9	-2	21	24	13		0	-21	103
							103
-14	2		16	26	6	30	5	13	0		105
	91								14
-14	3	1	2	12	11	35	8	16	0		100
									100
	105		115		115		121		114

F(x) = 3311

Таблица 6.5 – Цикл №3

	2		11		-3		13		0
-7	16	21	4		20	30	6		0	7	137
			108				29
11	3	-10	22		8		10	-14	0	-11	122
			7		115
0	19	17	9	-2	21	24	13		0		103
							92		11
0	2		16	5	6	9	5	-8	0		105
	102								3
0	3	1	2	-9	11	14	8	-5	0		100
									100
	105		115		115		121		114

F(x) = 3080

Таблица 6.6 – Цикл №4

	2		2		-12		4		0
2	16	12	4		20	30	6		0	-2	137
			16				121
20	3	-19	22		8		10	-14	0	-20	122
			7		115
0	19	17	9	7	21	33	13	9	0		103
									103
0	2		16	14	6	18	5	1	0		105
	102								3
0	3	1	2		11	23	8	4	0		100
			92						8
	105		115		115		121		114

F(x) = 2252

Таблица 6.7 – Цикл №5

	2		2		8		4		0
2	16	12	4		20	10	6		0	-2	137
			16				121
0	3	1	22	20	8		10	6	0		122
					115				7
0	19	17	9	7	21	13	13	9	0		103
									103
0	2		16	14	6	-2	5	1	0		105
	102								3
0	3	1	2		11	3	8	4	0		100
			99						1
	105		115		115		121		114

F(x) = 2112

Таблица 6.8 – Цикл №6

	4		2		8		4		0
2	16	10	4		20	10	6		0	-2	137
			16				121
0	3	-1	22	20	8		10	6	0		122
					112				10
0	19	15	9	7	21	13	13	9	0		103
									103
-2	2		16	16	6		5	3	0	2	105
	102				3
0	3	-1	2		11	3	8	4	0		100
			99						1
	105		115		115		121		114

F(x) = 2106

Таблица 6.9 – Цикл №7

	3		2		8		4		0
2	16	11	4		20	10	6		0	-2	137
			16				121
0	3		22	20	8		10	6	0		122
	102				10				10
0	19	16	9	7	21	13	13	9	0		103
									103
-2	2	1	16	16	6		5	3	0	2	105
					105
0	3	0	2		11	3	8	4	0		100
			99						1
	105		115		115		121		114

F(x) = 2004

Таблица 6.10– Оптимальный план грузоперевозок

	3		4		8		6		0
0	16	13	4		20	12	6		0		137
			15				121		1
0	3		22	18	8		10	4	0		122
	102				10				10
0	19	16	9	5	21	13	13	7	0		103
									103
-2	2	1	16	14	6		5	1	0	2	105
					105
-2	3	2	2		11	5	8	4	0	2	100
			100
	105		115		115		121		114

F(x) = 4*15 + 6*121 + 0*1 + 3*102 + 8*10 + 0*10 + 0*103 + 6*105 + 2*100  = 2002

Т. к. не осталось ни одной положительной сдвижки, то F=2002 – оптимальный план перевозок.

Результаты решения задачи с помощью макроса MC Excel «Поиск решение