Всякая невырожденная матрица (DA╧0) квадратная матрица A имеет так называемую обратную матрицу. Матрица B называется обратной по отношению к матрице A, если произведение AB равно единичной матрице: AB = E. Для матрицы, обратной по отношению к матрице A, вводят обозначение A-1 Обратная матрица находится по формуле
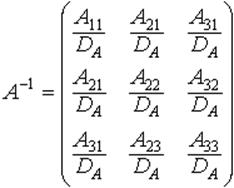
где Amn алгебраическое дополнение элемента матрицы amn в ее определителе, т.е. произведение минора второго порядка, полученного вычеркиванием m-й строки и n-го столбца в определителе матрицы A, на (-1)m+n При умножении матриц A и A-1 выполняется переместительный закон, т.е. AA-1=A-1A=E
Для прямоугольной матрицы определена операция транспонирование. Матрица, получающаяяся путем замены строк столбцами называется транспонированной по отношению к исходной матрице. Транспонированная матрица обозначается как AT
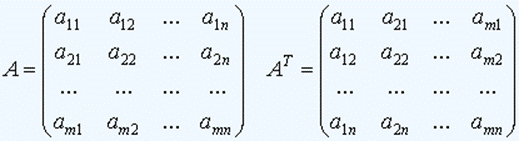
При транспонировании матрицы верны следующие соотношения:
(AT)T = A (A+B)T = AT+BT (AB)T = BTAT
Квадратная матрица A, для которой AT = A, называется симметричной. Элементы такой матрицы, расположенные симметрично относительно главной диагонали равны.
Определителем второго порядка, соответствующим таблице элементов
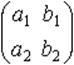
называется число a1 b2 - a2 b1. Определитель второго порядка обозначается так:
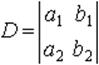
Таким образом,
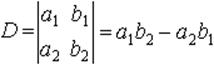
Определитель третьего порядка, соответствующий таблице элементов
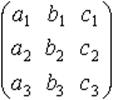
определяется равенством
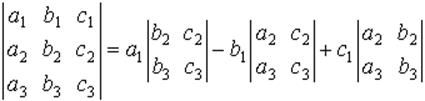
Теперь оставим теорию и приступим к практике. Для начала научимся задавать правильно матрицы в Excel.
Что такое матрица с точки зрения MS Excel?
В MS Excel при выполнении действий над векторами и матрицами используется понятие массива. Под массивом понимается некоторый диапазон ячеек, для которых установлены единые правила обработки, например формулы расчета отдельных элементов. Одномерный массив может рассматриваться как вектор, а двумерный - как матрица. Формулы для массива вводятся несколько иначе, чем для обычной ячейки. Отличие состоит в двух обстоятельствах:
ü перед вводом формулы (МОПРЕД, МУМНОЖ, МОБР, ТРАНСП) диапазон ячеек должен быть выделен. Этот диапазон будет результирующим;
ü ввод формулы завершается одновременным нажатием трех клавиш Ctrl+Shift+Enter.
Массивы передаются в качестве аргументов математическим функциям. В некоторых случаях результатом выполнения функции также является массив. Рассмотри пример - умножение матриц, а заодно научимся некоторым принципам работы с матрицами в MS Excel.
В MS Excel существует достаточно большое количество встроенных функций: МОПРЕД, МУМНОЖ, МОБР, ТРАНСП. Ознакомиться с ними можно в справочной системе MS Excel. Далее будут описаны основные из них.
Для начала зададим матрицу в MS Excel:
ü Для этого выделим диапазон A1:C3, размером 3х3 ячейки, в строке ввода наберите число 1 и нажмите одновременно клавиши Ctrl+Shift+Enter. Все выделенные ячейки получат значение, равное 1. Аналогично сформируем другой массив со значениями, равными 2.
ü Научимся формировать массивы на основе формул. Для этого выделите на свободном пространстве диапазон, размером 3х3 ячейки, в строке ввода наберите формулу =A1:C3*5 и нажмите одновременно клавиши Ctrl+Shift+Enter. Обратите внимание, что формула автоматически заключилась в фигурные скобки, что указывает на зону ее действия - массив, а все ячейки нового массива получили значения в 5 раз больше ячеек первого массива. Данное действие можно рассматривать как умножение матрицы на скаляр.
ü Выделим диапазон A5:C7 – это матрица будет результатом транспонированной матрицы. Используя функцию ТРАНСП, транспонируем эту матрицу. Для этого выберем значок функции fx на панели (рис. 1):
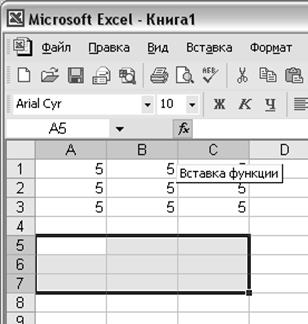
Рисунок 1
И в появившемся окне (рис. 2):
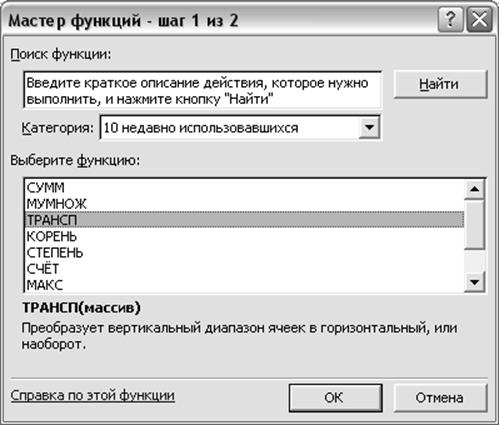
Рисунок 2
Найти функцию ТРАНСП() и нажать ОК. в появившемся диалоге (рис. 3):
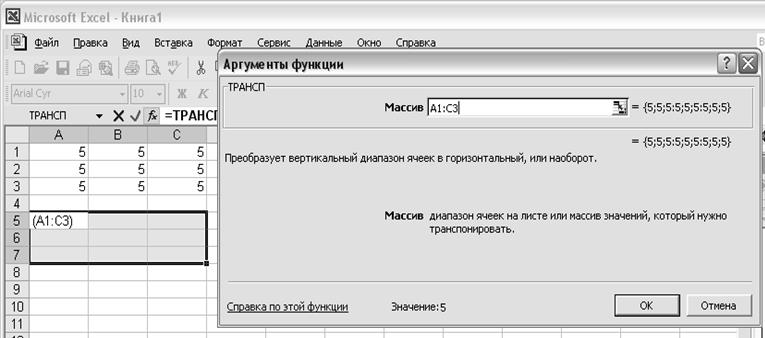
Рисунок 3
Выбрать диапазон A1:C3 и нажать Ctrl+Shift+Enter. Мы увидим транспонированную матрицу.
ü Облегчить работу при работе с матрицами можно, если задавать
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.