












предполагаемое значение и повторно запустить надстройку Поиск решения.
Необходимо решить систему уравнений
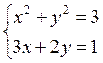
Система содержит уравнение окружности и уравнение прямой. Решением этой системы являются точки пересечения окружности с прямой. При этом прямая может пересечь окружность в двух точках, коснуться окружности в одной точке или не пересечь окружность вовсе. Таким образом, решений этой системы может быть не более двух или не быть вообще. Пара (х, у) является решением системы уравнения в том случае, если она является решением уравнения с двумя неизвестными:
![]()
Левая часть этого уравнения представляет собой функцию от двух переменных. Чтобы решить уравнение, нужно протабулировать эту функцию. За начальные приближения к корням уравнения следует выбрать пары (х, у), в которых функция ближе всего к нулю (рис. 8).
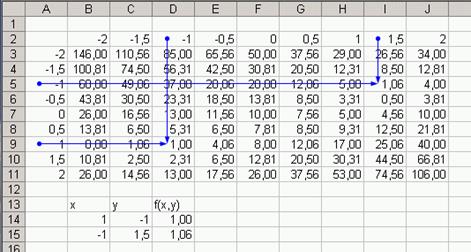
Рис. 8 Решение системы нелинейных уравнений
На рис. 8 в диапазоне A2:J11 представлена таблица значений функции двух переменных. В столбце А этого диапазона находится аргумент х, в строке 2 - аргумент у. Значения функции равные 1 (при х = 1 и у = -1) и 1,06 (при х = -1 и у = 1,5) расположены ближе всего к значению 0 (по сравнению с другими значениями функции). Эти две пары были взяты за первое приближение корней. В диапазон В14:С14 была помещена первая пара, а в диапазон В15:С15 - вторая В диапазоне D14:D15 введены формулы, реализующие левую часть уравнения, формула в ячейке D14 использует значения из диапазона В14:С14, а формула в ячейке D15 -из диапазона В15:С15
Чтобы найти первый корень, нужно выделить ячейку D14, вызвать окно Поиск решения и заполнить его, как показано на рис. 9.
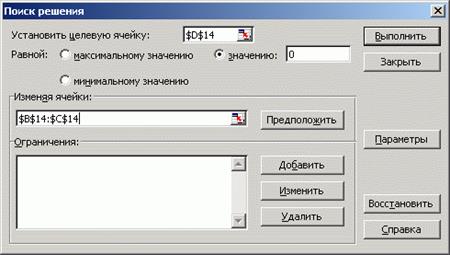
Рис. 9 Поиск решения системы нелинейных уравнений
В рассмотренной задаче ограничения отсутствуют. В диалоговом окне Параметры поиска решения флажок Линейная модель должен быть сброшен. После нажатия кнопки Выполнить будет найден первый корень. Чтобы найти второй корень, потребуется вызвать Поиск решения для второй пары. На рис. 10 в диапазоне B13.D15 приведен результат решения задачи.
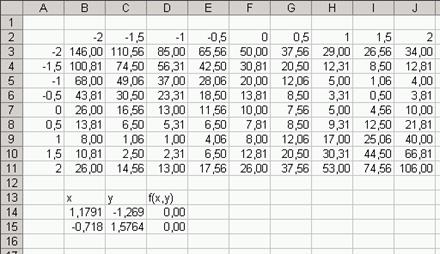
Рис. 10 Результат решения системы уравнений
Надстройку Поиск решения можно использовать для решения задач оптимизации. В качестве простого примера рассмотрим уравнение
![]() .
.
На рис. 11 представлен график функции, определяемой уравнением. Эта функция имеет максимум равный 26 при x = 4.
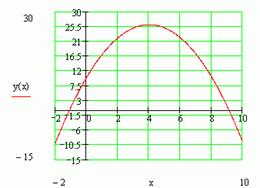
Рис. 11 График функции
Чтобы найти максимум этой функции с помощью надстройки Поиск решения, введем в одну ячейку таблицы правую часть уравнения, а в другую — предполагаемое значение переменной х (рис. 12).
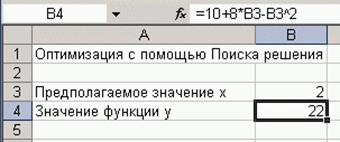
Рис. 12 Задание начальных значений
Задав в диалоговом окне Поиск решения указанные на рис. 13 параметры, найдем максимум. Соответствующее значение переменной x: отображается в ячейке ВЗ (рис. 13).
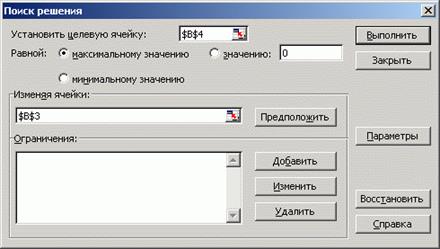
Рис. 13 Окно Поиска решений
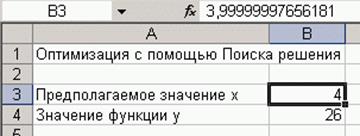
Рис. 14 Результаты поиска решения
В результате работы надстройки Поиск решения получилось значение 3,99999997656181, несколько отличающееся от 4 (рис. 14). Надстройка прекращает работу, когда достигнута заданная точность (precision). Чтобы установить необходимую точность, воспользуйтесь кнопкой Параметры, расположенной в диалоговом окне Поиск решения.
В области, заданной условиями ![]() и
и ![]() , функция
, функция ![]() имеет
максимум в точке x=1.5708 (или
имеет
максимум в точке x=1.5708 (или ![]() )
и y=0.
)
и y=0.
Чтобы найти с помощью надстройки Поиск решения координаты x и y максимума функции f(x,y), введите в ячейки предполагаемые значения координат и рассматриваемую функцию (рис. 15).
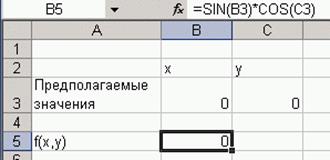
Рис. 15
Задайте в диалоговом окне Поиск решения параметры, необходимые для
нахождения значений x и y, в
которых формула в ячейке B5 имеет максимум. Так как у
рассматриваемой функции бесконечное количество максимумов, необходимо
ограничить область поиска условиями ![]() и
и ![]() (рис. 16).
(рис. 16).
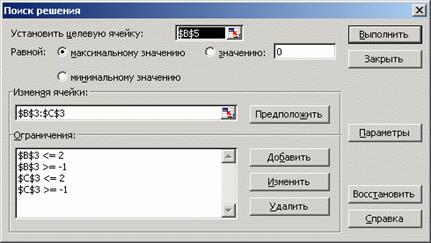
Рис. 16
Результаты поиска решения верны (рис. 16).
В заданной области у рассматриваемой функции имеется также локальный максимум в точке x=-1 y=2. Если задать в качестве нулевого приближения точки около этого локального максимума (например x=-0.9 y=1.8), то надстройка найдет значение этого локального максимума.
Следует помнить о том, что найденные решения нуждаются в проверке. Один из способов проверки решения - построение графика исследуемой функции.
1. Для решения каких задач применяют средство Поиск решения?
2. Опишите процесс подготовки задачи к решению с помощью средства Поиск
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.