Влияние параметров цепи на скорость протекания процесса. Измерение параметров цепи по осциллограмме переходного процесса, страница 3

            Решение дифференциального уравнения находим как сумму составляющей установившегося режима  и свободной составляющей :

.

            Составляющая установившегося режима  определяется видом заданной функции , и для случая заряда катушки имеет вид , а для случая разряда .

            Постоянная интегрирования  определяется из начальных условий. Для случая заряда катушки: , а для случая разряда катушки: .

            Таким образом, при включении катушки индуктивности последовательно с источником постоянного напряжения переходной  процесс описывается функциями:

            При включении катушки индуктивности с запасенной энергией последовательно с сопротивлением переходной процесс описывается функциями:

            При этом энергия, выделяемая на сопротивлении при разряде, равна энергии, запасенной в магнитном поле катушки индуктивности:

.

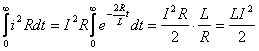            Зависимости мощности, выделяемой на катушке индуктивности, и запасаемой энергии от времени при включении последовательно с источником постоянного напряжения выглядят так:

            На Рис.2  построены графики теоретических зависимостей соответственно мощности  и энергии от времени при включении катушки последовательно с источником постоянного напряжения.

Рис. 3 Графики теоретических зависимостей выделяемой мощности  и запасаемой энергии в катушке

            При заряде катушки постоянна времени переходного процесса равна:

            А при разряде катушки постоянная времени равна:

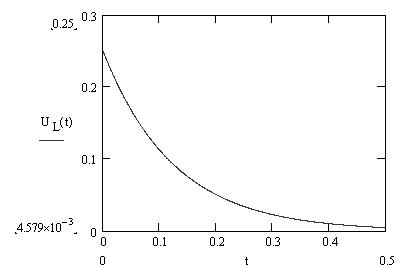
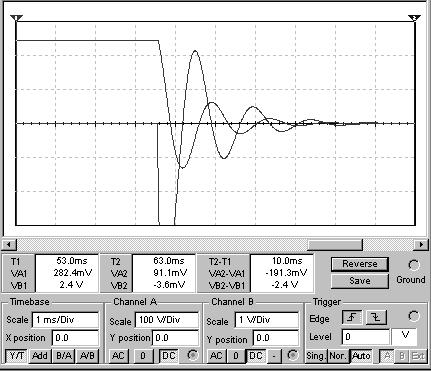
            Следовательно, переходной процесс разряда катушки идет в два раза быстрее, чем процесс заряда, что хорошо видно на Рис.4 и Рис.5 а так же Рис.6 и Рис.7, на которых представлены осциллограммы колебаний тока цепи и напряжения на катушке а так же мощности катушки и энергии.