Влияние параметров цепи на скорость протекания процесса. Измерение параметров цепи по осциллограмме переходного процесса, страница 2

.

Решение дифференциального уравнения, описывающего переходной процесс, находим в виде:

,

где  – установившееся значение напряжения конденсатора, равное  ( – значение ЭДС источника);  – постоянная интегрирования, определяемая из начальных условий: .

Таким образом, решив дифференциальное равнение переходного процесса,  получим функции напряжения и тока рассматриваемой цепи при зарядке конденсатора:

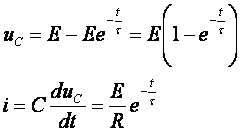
В момент коммутации напряжение конденсатора равно нулю, а ток в цепи изменяется скачком от нуля до . Таким образом, в момент переключения ключа величина тока полностью определяется значениями ЭДС источника и активного сопротивления цепи.

При разрядке конденсатора на сопротивление R свободная составляющая равна нулю (), а постоянная интегрирования . Тогда переходной процесс разрядки конденсатора описывается уравнениями:

          

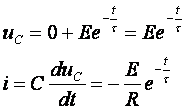
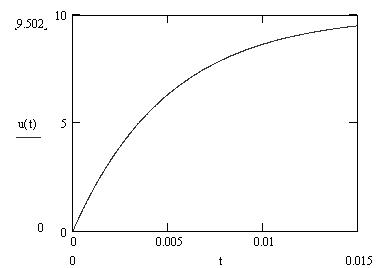
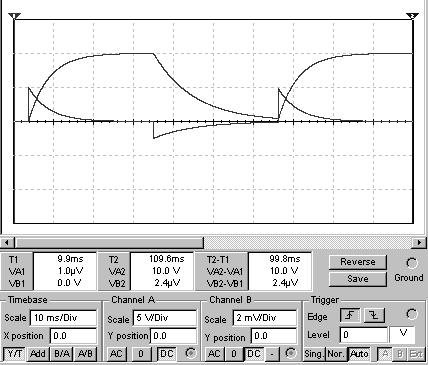
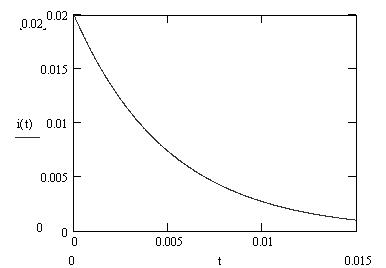
График 1 зависимости i(t) u(t)

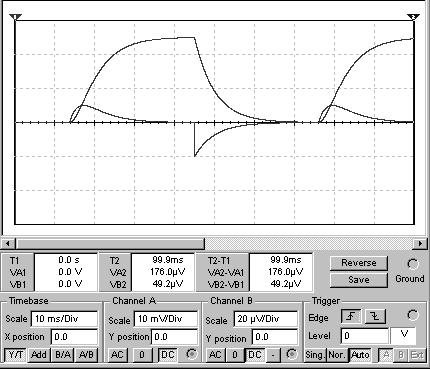
График 2 зависимость E(t) W(t)

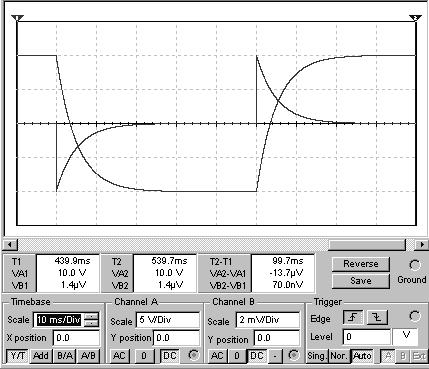
График 3  Вследствие изменения тока изменяется и амплитуда , которая возрастает в 2 раза при увеличении тока в 2 раза

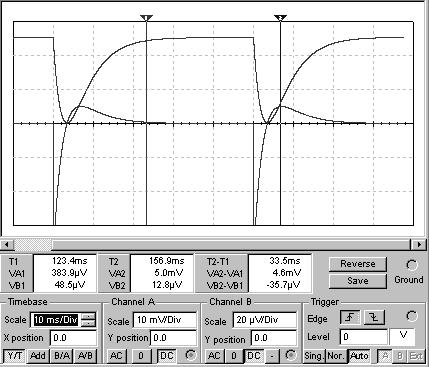
График 4 На схеме показан график перезарядки конденсатора.

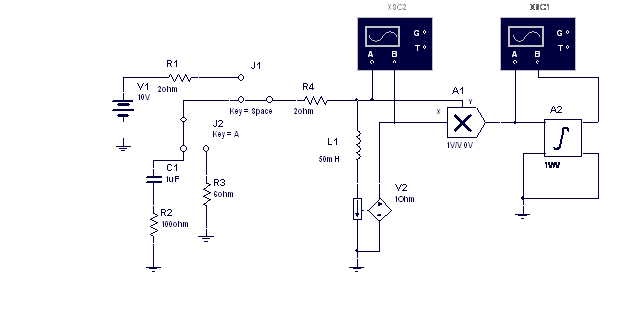
Заряд и разряд катушки индуктивности в последовательной RL-цепи.

            Нулевые начальные условия:

.

            Из закона Кирхгофа для напряжения с учетом  получим дифференциальное уравнение первого порядка , описывающее переходной процесс заряда катушки индуктивности:

.

            Определим соответствующее ему однородное уравнение:

,

где –  свободная составляющая тока.

            Характеристическое уравнение  имеет единственный корень , таким образом:

.

             – постоянная времени, показывающая за какой промежуток времени ток убывает в раз.