Методические указания
1. Построение и экономико-математический анализ моделей межотраслевого баланса
Задача 1.
1.1. Недостающие величины в шахматной таблице МОБ находятся из основных балансовых соотношений:
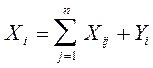 ,
, ![]() (1)
(1)
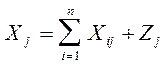 ,
, ![]() (2)
(2)
где Xi - валовой выпуск продукции i-й отрасли; Xij - производственное потребление продукции i-й отрасли в j-й отрасли; Yi - конечная продукция i-й отрасли; Zj- добавленная стоимость, созданная в j-й отрасли; n- количество отраслей. Конечная продукция i-й отрасли Yi , например, может включать:
* личное потребление населения;
* прирост запасов и резервов;
* капитальные вложения, возмещение потерь и выбытия основных производственных фондов;
* экспортно-импортное сальдо, т.е. разность между экспортом и импортом продукции данной отрасли.
Добавленная стоимость j-й отрасли (Z)j определяется как разность между стоимостью валового выпуска и всеми материальными затратами j-й отрасли. Основными составляющими добавленной стоимости являются:
* годовая заработная плата, начисленная всем занятым в этой отрасли рабочим и служащим с учетом отчислений во внебюджетные фонды;
* амортизация, начисленная в j-й отрасли за год;
* годовая прибыль всех предприятий данной отрасли и т.д.
Используя формулы (1), (2) последовательно находим:
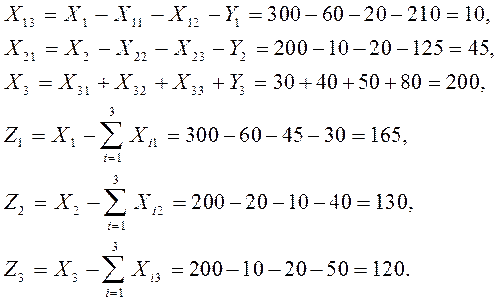
Таким образом, шахматная таблица МОБ примет вид (табл. 3)
Таблица 3
|
продукции Затраты на производство |
Производственное потребление в отраслях |
Конечный продукт |
Валовой выпуск |
||
|
Промышленность |
Сельское и лесное хозяйство |
Прочие отрасли |
|||
|
Промышленность |
60 |
20 |
10 |
210 |
300 |
|
Сельское и лес. хоз-во |
45 |
10 |
20 |
125 |
200 |
|
Прочие отрасли |
30 |
40 |
50 |
80 |
200 |
|
Добавленная стоимость |
165 |
130 |
120 |
||
|
Валовой выпуск |
300 |
200 |
200 |
||
|
Труд. рес. (млн. чел.-лет) |
18 |
15 |
25 |
||
|
Осн. Фонды (млрд. руб.) |
450 |
100 |
250 |
||
1.2. Коэффициенты прямых затрат aij определяются по формуле:
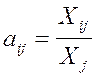 . (3)
. (3)
Тогда 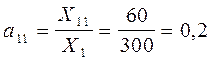 ;
;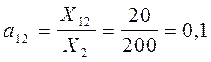 ;
; 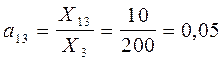 и
т.д., а матрица прямых затрат A=(aij) примет вид
и
т.д., а матрица прямых затрат A=(aij) примет вид
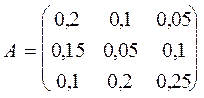 .
.
Коэффициенты прямой трудоемкости (tj) и прямой фондоемкости (fj ) продукции j-й отрасли находятся по формулам:
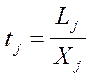 ;
; 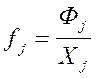 ; (4)
; (4)
где
Lj - трудовые ресурсы j-й отрасли; ![]() - основные производственные фонды j-й отрасли. По формулам (4) находим:
- основные производственные фонды j-й отрасли. По формулам (4) находим:
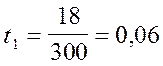 ;
; 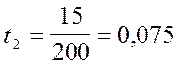 ;
; 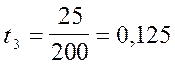 ,
,
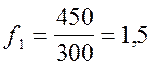 ;
; 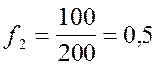 ;
; 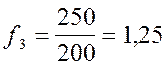 .
.
Содержательный смысл найденных коэффициентов aij, tj, fj состоит в следующем. a12=0,1 означает, что для производства продукции сельского и лесного хозяйства на 1 млн. руб. необходимо затратить продукции промышленности на 100 тыс. руб. (удобрения, гербициды, горюче-смазочные материалы, зап. части и т. д.). Так, t1 =0,06 означает, что для производства продукции промышленности на 1 млрд. руб. необходимо использовать в этой отрасли 60 тыс. чел.-лет трудовых ресурсов. Так, f2 =0,5 означает, что для производства продукции сельского и лесного хозяйства на 1 млрд. руб. в этой отрасли должно быть задействовано основных производственных фондов на 500 млн. руб. (здания, сооружения, транспорт, комбайны, оборудование и т. д.).
1.3. Линейная статическая модель межотраслевого баланса имеет вид
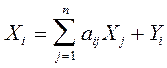 , (5)
, (5)
или в матричной форме
![]() , (6)
, (6)
где ![]() - вектор валовых выпусков
отраслей, A=(aij) - матрица коэффициентов прямых затрат,
- вектор валовых выпусков
отраслей, A=(aij) - матрица коэффициентов прямых затрат, ![]() - вектор конечной продукции. В нашем
примере система (5) запишется следующим образом
- вектор конечной продукции. В нашем
примере система (5) запишется следующим образом
![]()
![]() (7)
(7)
![]() .
.
Математическая модель (5) представляет собой систему n линейных уравнений, в которой неизвестными величинами могут быть как Xi, так и Yi. Очевидно, что такая система может иметь единственное решение только в том случае, когда число неизвестных величин не превышает числа уравнений. Принятие одних величин за известные, а других - за неизвестные определяется постановкой конкретной экономической задачи. Типовыми являются следующие задачи:
1. Определение объемов валового выпуска по заданным объемам конечной продукции.
2. Определение объемов конечной продукции по данным об объемах валового выпуска.
3. Определение объемов валового выпуска по одним видам продукции и объемов конечной продукции по другим видам.
В соответствии с условием задачи 1.3. нам необходимо найти вектор валовых выпусков X по заданному вектору конечной продукции Y, т.е. решить первую из вышеперечисленных типовых задач.
Рассмотрим систему (6), т.е. ![]() ,
и запишем ее в несколько ином виде, сделав ряд эквивалентных преобразований:
,
и запишем ее в несколько ином виде, сделав ряд эквивалентных преобразований:
![]() , где I
- единичная матрица порядка n,
у которой на главной диагонали расположены единицы, а остальные элементы -
нули. Таким образом, система (6) может быть представлена следующим образом:
, где I
- единичная матрица порядка n,
у которой на главной диагонали расположены единицы, а остальные элементы -
нули. Таким образом, система (6) может быть представлена следующим образом:
![]() . (8)
. (8)
Если существует матрица, обратная к матрице (I - A), т.е., если существует матрица (I - A)-1, то решение X системы (8) может быть найдено по формуле:
![]() . (9)
. (9)
Напомним, что обратной к квадратной матрице D называется такая матрица (обозначается D-1), которая удовлетворяет соотношениям:
![]() .
.
Матрица (I - A)-1
называется матрицей полных затрат и обычно обозначается через В, т.е. ![]() . Элементы bij матрицы В называются коэффициентами полных затрат и
имеют важнейшее значение при исследовании и анализе взаимодействия отраслей
национальной экономики.
. Элементы bij матрицы В называются коэффициентами полных затрат и
имеют важнейшее значение при исследовании и анализе взаимодействия отраслей
национальной экономики.
Найдем матрицу полных затрат для модели (7). Алгоритм нахождения обратной матрицы к произвольной квадратной матрице D=(dij) состоит из следующих этапов
1. Находится определитель матрицы D, который обозначается |D|. Если |D| ¹ 0, то обратная матрица D-1 существует; в противном случае матрица D-1 не может быть
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.