Решение матричных игр в среде EXCEL

Федеральное агентство по образованию

Новосибирский государственный университет

экономики и управления

Кафедра ЭММ и П

Лабораторная работа №4

по курсу экономико-математических методов, на тему:

«Решение матричных игр в среде EXCEL»

                                       Выполнила студентка гр.4046

Желтова Е.А.

Проверил: Доцент кафедры

 ЭММиП Савиных В.Н.

Новосибирск,2006

План лабораторной работы.

1. Составление моделей, отражающих интересы игроков.
2. Решение моделей, отражающих интересы игроков, как задачи ЛП в среде EXCEL.
3. Анализ результатов расчетов и их экономическая интерпретация.

1. Составление моделей, отражающих интересы игроков.

Графический анализ матричной игры

Для второго игрока смешанной стратегией будит вектор Q=(q1,q2,q3,q4)

0<=qj<=1

j=1,2,3,4.

q1+q2+q3+q4=1

Тогда средний выигрыш первого игрока:

1-й ход: 4q1-7q2+5q3-7q4<=V

2-й ход: -4q1+7q2-11q3+8q4<=V

V->min

Для первого игрока смешанной стратегией будит вектор      P=(p1,p2)

0<=pi<=1

i=1,2.

p1+p2=1

Тогда средний выигрыш первого игрока:

1-й ход: 4p1-4p2>=V

2-й ход: -7p1+7p2>=V

3-й ход: 5p1-11p2>=V

4-й ход: -7p1+8p2>=V

V-> max  

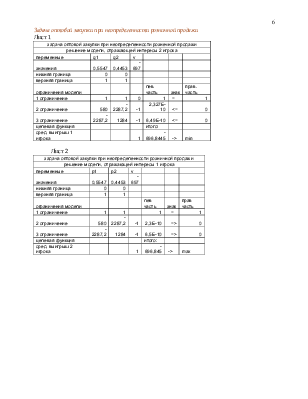
Задача оптовой закупки при неопределенности розничной продажи

Для второго игрока смешанной стратегией будит вектор

Q=(q1,q2)

0<=qj<=1

j=1;2

q1+q2=1

Тогда средний выигрыш  первого игрока:

1-й ход: 580q1-2287,2q2<=V

2-й ход: -2287,2q1+1284q2<=V

V->min

Для первого игрока смешанной стратегией будит вектор

P=(p1,p2)

0<=pi<=1

i=1;2

p1+p2=1

Тогда средний выигрыш первого игрока:

580p1-2287,2p2>=V

-2287,2p1+1284p2>=V

V->max

Задача выбора структуры посевов

2.Решение моделей, отражающих интересы игроков, как задачи ЛП в среде EXCEL.

В EXCEL задача составляется на двух листах. На первом отражены интересы второго игрока, а на втором- первого. На первом листе в ячейки B4:F4 заносятся значения, равные 1. Следующая строка- это нижняя граница, равная 0, а следующая строка- верхняя граница, равная 1. В ячейки B8:F10 заносятся ограничения модели. В левую часть заносится формула сумма произведений. В правую часть в первом ограничении заносится 1, в остальные два- 0. Знак в первом ограничении =, а в остальных- <=. Целевая функция на минимум.

   На втором листе в ячейки B4:D4 заносятся 1. Также пишется верхняя и нижняя граница.  В ячейки B8:C12  заносятся 5 ограничений модели. Левая и правая части аналогичны первому листу. Знак первого ограничения- =, а остальные- >=. Целевая функция на максимум.

           Для составления компьютерного  аналога математической модели используется надстройка «поиск решений». Для вызова окна надстройки необходимо обратиться в меню сервис/поиск решений.

            Для запуска вычислительного процесса необходимо нажать кнопку ВЫПОЛНИТЬ, после чего в случае верного решения появляется окно «Результаты поиска решения». При этом на рабочем листе происходят соответствующие изменения найдены оптимальные значения переменных, в целевой ячейке – минимальное значение целевой функции, а на втором листе- максимальное. Внизу экрана появился корешок – отчет по результатом.

3.Анализ результатов расчетов, и их экономическая интерпретация.

Графический анализ матричной игры

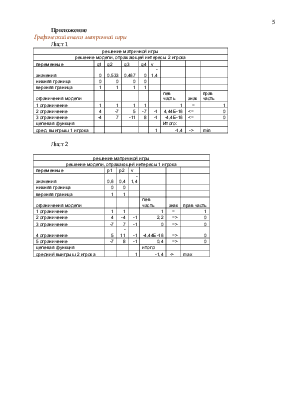
P=(0,6; 0,4)

Это означает, что первый игрок должен делать 1-й ход с вероятностью 0,6,  а  2-й с вероятностью 0,4.

V=-1,4 - это означает, что первый игрок проиграет второму 1,4 ед. , и это будет его минимальный проигрыш.

Q=(0; 0,533; 0,467; 0)

Это означает, что второй игрок должен делать 2-й ход с вероятностью 0,533, 3-й ход с вероятностью 0,467, а первым и четвертым он не должен пользоваться

V=-1,4 – это означает, что второй игрок выиграет 1,4 ед. , и это будет его минимальный выигрыш.

Задача оптовой закупки при неопределенности розничной продажи

P=(0,5547; 0,4353)

Это означает, что фирма будет рассчитывать на дождь с вероятностью 0,5547, а на солнце с вероятностью 0,4353.

V= -697 – это означает, что фирма потерпит убытки в размере 697 рублей, и это будит ее минимальный проигрыш.

Q=(0,5547; 0,4353)

Это означает, что дождь будит с вероятностью 0,5547, а солнце с вероятностью 0,4353.

Задача выбора структуры посевов

Приложение

Графический анализ матричной игры

Лист 1