
























































проецирования, а чертежи, построенные по этому методу, называются проекционными.
В практике проецирования используются два способа:
1. Центральное проецирование.
2. Параллельное проецирование, как наиболее распространенное в инженерной графике.
Центральное проецирование
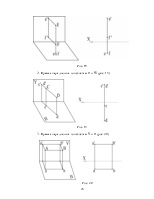
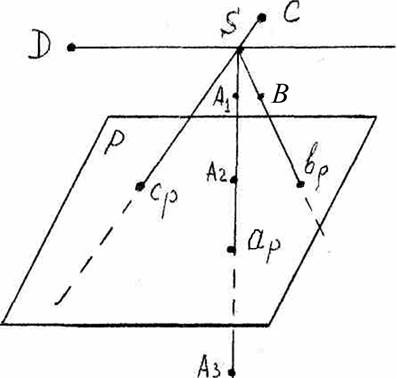 Для получения центральных проекций (центральное
проецирование) надо задаться плоскостью проекций и центром проекций – точкой,
не лежащей в этой плоскости (Рис. 1: P – плоскость проекций; S – центр проекций –
точка).
Для получения центральных проекций (центральное
проецирование) надо задаться плоскостью проекций и центром проекций – точкой,
не лежащей в этой плоскости (Рис. 1: P – плоскость проекций; S – центр проекций –
точка).
Рис. 1
Взяв некоторую точку А и проведя, через S и A1 прямую линию до пересечения ее с плоскостью Р, получим точку ар , Также поступаем, например, с точками В и С. Точки ар, вр, ср являются центральными проекциями точек A1, В, С на плоскость Р: они получаются в пересечении проецирующих прямых (лучей) SA1, SB, SС с плоскостью проекций Р.
Очевидно, если изменить центр проекций, то получатся новые проекции точек на плоскость Р.
На примере центрального проецирования основано фотографирование, кинопроектирование и выполнение чертежей способом линейной перспективы. Линейная перспектива применяется в архитектуре.
Параллельное проецирование
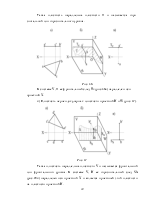
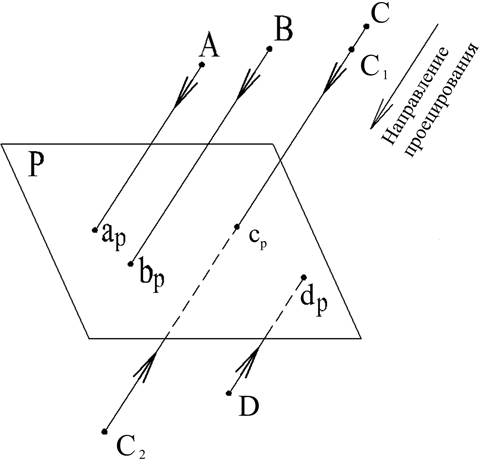 При параллельном
проецировании считается, что центр проекций отсутствует, а есть только
направлении проецирования. При этом все проецирующие прямые (лучи) параллельны
между собой и параллельны заданному направлению (рис. 2).
При параллельном
проецировании считается, что центр проекций отсутствует, а есть только
направлении проецирования. При этом все проецирующие прямые (лучи) параллельны
между собой и параллельны заданному направлению (рис. 2).
Рис. 2
Следовательно, параллельной проекцией точки будем называть точку пересечения проецирующей прямой, проведенной параллельно заданному направлению, с плоскостью проекций.
Рассмотрим свойства параллельного проецирования.
1. Каждой точке пространства соответствует одна проекция этой точки на плоскости проекций (рис. 2: А, В, С).
2. Одна проекция не определяет положение точек в пространстве (рис. 2: С C1, С2).
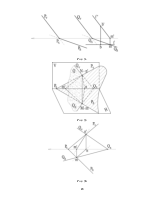
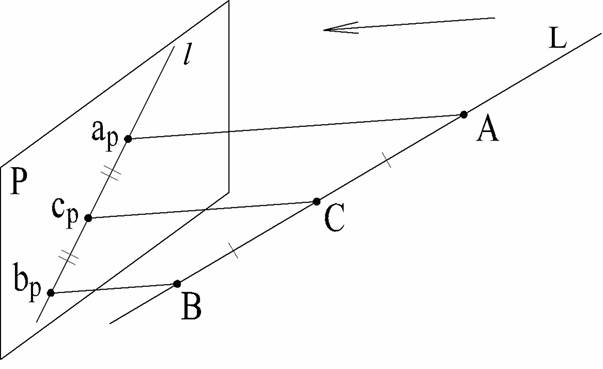 3. Проекция прямой есть прямая (рис. 3). Действительно, проецирующие
лучи, проходящие через точки прямой L (рис. 3: А, В, С), образуют плоскость, которая пересекается
с плоскостью проекций Р по линии l. Эта линия является проекцией прямой L.
3. Проекция прямой есть прямая (рис. 3). Действительно, проецирующие
лучи, проходящие через точки прямой L (рис. 3: А, В, С), образуют плоскость, которая пересекается
с плоскостью проекций Р по линии l. Эта линия является проекцией прямой L.
Рис. 3
4. Если пространственный отрезок прямой АВ разделить в заданном отношении (рис. 3 – отрезок АВ точкой С делится пополам), то и проекция этого отрезка ар вр разделится в том же отношении. Это очевидно, если вспомнить теорему о пропорциональности отрезков прямых между параллельными прямыми (параллельные проецирующие лучи).
5. Проекции параллельных линий параллельны между собой (если две параллельные плоскости пересечь третьей плоскостью, то линии пересечения этих плоскостей будут параллельны).
6. Каждая линия на плоскости проекций может быть проекцией множества линий, если они расположены в общей для них проецирующей плоскости (рис. 4)
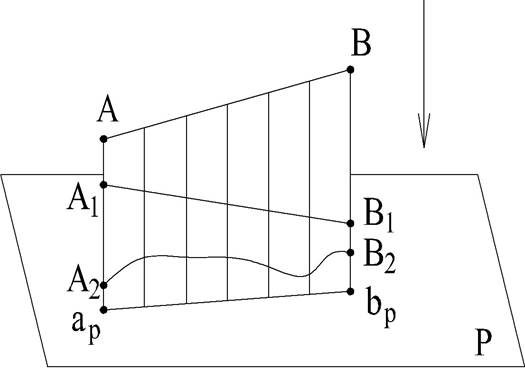
Рис. 4
Отрезок арвр служит проекцией отрезков АВ, A1B1 и отрезка плоской кривой A2B2.
7. Для построения проекции прямой достаточно спроецировать две ее точки и через полученные проекции этих точек провести прямую линию.
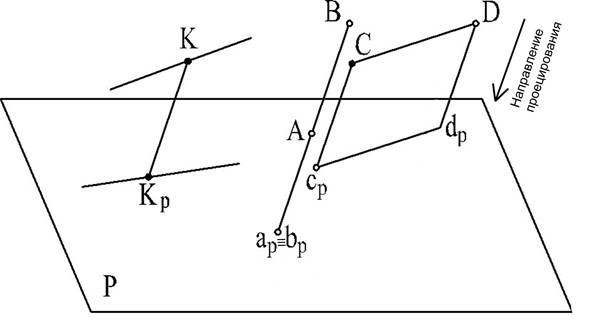 8. Если точка принадлежит прямой, то проекция точки принадлежит
проекции этой прямой (рис. 5: точка К принадлежит прямой, кр
принадлежит проекции этой прямой).
8. Если точка принадлежит прямой, то проекция точки принадлежит
проекции этой прямой (рис. 5: точка К принадлежит прямой, кр
принадлежит проекции этой прямой).
Рис. 5
9. Если прямая параллельна направлению проецирования (рис. 5, прямая АВ), то проекцией прямой (и любого ее отрезка) является точка (ар совпадает с вр).
10. Отрезок прямой линии, параллельной плоскости проекций, проецируется на эту плоскость в натуральную величину (рис. 5: CD = cpdp как отрезки параллельных прямых).
Из рассмотренных свойств следуют два очень важных следствия:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.