В результате расчетов мы получили отрицательную длительность работы А6(3-4). Это значит, что мы пытаемся перенести на эту работу средств больше, чем она может освоить. Следовательно, предлагаемый вариант переноса средств не корректен. Но раз есть избыток средств, то их следует распределить между большим числом работ. Например, переносить средства с работы А3(1-4) находящейся на подкритическом пути L3 на работы А10(6-7), А5(2-3) и А6(3-4), находящихся на критических путях. При этом число переменных увеличится до четырёх: Х1,4; Х6,7; Х2,3; Х3,4. Число уравнений останется равным трем, так как число критических путей осталось тем же.
|
t min=t1,4(1-с1,4* Х1,4 )
|
Решая эту работу относительно Х1,4 , получим
|
Х1,4 =1/ с1,4 (1- tmin/ t1,4)
|
Х1,4 =1/0,3(1-0,5/1)=3,333*0,5=1,667
Рациональнее всего выбрать те работы, которые могут освоить наибольшее количество средств.
Рассчитаем Х max для всех работ, которые могут участвовать в оптимизации, расчеты сведем в таблице 3.
Таблица 3.
|
Работа |
А2(1-7) |
А3(1-4) |
А4(1-2) |
А5(2-3) |
А6(3-4) |
А7(4-7) |
А8(3-5) |
А9(5-6) |
А10(6-7) |
|
Хi,j |
4,17 |
1,666 |
1,875 |
1,25 |
1,666 |
1,299 |
0,757 |
0,972 |
2,223 |
Проанализировав результаты расчетов таблицы 3, выбираем работы, которые могут освоить максимальное количество средств: А4(1-2); А5(2-3); А6(3-4) и А10(6-7). Запишем новую систему уравнений
![]()
Х1,4 = Х1,2+ Х2,3+ Х3,4+ Х6,7
Т3+ t1,4*с1,4* Х1,4= Ткр-( t1,2*с1,2* Х1,2+ t2,3*с2,3* Х2,3+ t6,7*с6,7* Х6,7)
Т3+ t1,4*с1,4* Х1,4= Ткр-( t1,2*с1,2* Х1,2+ t2,3*с2,3* Х2,3+ t3,4*с3,4* Х3,4)
![]() Подставим значения
Подставим значения
Х1,4 = Х1,2+ Х2,3+ Х3,4+ Х6,7
27,05+1*0,3* Х1,4 =33,5-(2*0,6*1,875+2*0,6*1,25+1,5*0,3* Х6,7)
27,05+1*0,3* Х1,4 =33,5-(2*0,6*1,875+2*0,6*1,25+3*0,5*Х3,4)
Полученное решение имеет следующий вид:
Х1,4=5,257
Х3,4=0,45
Х6,7=1,682
Проверим на допустимость переносимых средств:
5,257<= 20 – решение допустимо.
Найдем новые длительности работ:
t′1,4= t1,4(1+с1,4*х1,4)
t′1,2=t1,2(1-с1,2*х1,2)
t′2,3=t2,3(1-с2,3*х2,3)
t′3,4=t3,4(1-с3,4*х3,4)
t′6,7=t6,7(1-с6,7*х6,7)
t′1,4=1(1+0,3*5,257)=2,577
t′1,2=2(1-0,4*1,875)=0,5
t′2,3=2(1-0,6*1,25)=0,5
t′3,4=3(1-0,5*0,45)=2,325
t′6,7=1,5(1-0,3*1,682)=0,743
Определяем новые длительности путей, суммируя длительности работ, входящих в соответствующие пути:
Т1=6+0,5+0,5+3+4+0,743+3+5+7=29
Т2=6+0,5+0,5+0,325+5,5+3+5+7=29
Т3=6+2,554+5,5+3+5+7=29
Т4=6+3+3+5+7=24
Прейдем к третьему, последнему этапу оптимизации. Не критический путь Т4. Резерв времени 5 дней. Будем переносить средства с работы А2(1-7) на А9(5-6), А7(4-7)
|
Х1,7<= r1,7 /t1,7*c1,7
Х1,7<= 5/(3*0,2)
Х1,7<= 8,333
Запишем систему уравнений, с помощью которой можно определить величину переносимых средств:
![]() Х1,7=Х1,4+Х4,7+Х5,6
Х1,7=Х1,4+Х4,7+Х5,6
Т4+ t1,7*с1,7* Х1,7=Ткр- t1,4*с1,4* Х1,4
Т4+ t1,7*с1,7* Х1,7=Ткр- t4,7*с4,7* Х4,7
Т4+ t1,7*с1,7* Х1,7=Ткр- t5,6*с5,6* Х5,6
Подставляем значения
![]() Х1,7=Х3,5+Х4,7+Х5,4
Х1,7=Х3,5+Х4,7+Х5,4
24+ 3*0,2* Х1,7=29- 3*1,1* Х3,5
24+ 3*0,2* Х1,7=29- 5,5*0,7* Х4,7
24+ 3*0,2* Х1,7 =29- 4*0,9* Х5,6
Полученное решение имеет следующий вид:
Х1,7=
Х3,5=
Х4,7=
Х5,6=
Проверим на допустимость переносимых средств:
<= 20 – решение допустимо.
Найдем новые длительности работ:
t′1,7= t1,7(1+с1,7*х1,7)
t′3,5=t3,5(1-с3,5*х3,5)
t′4,7=t4,7(1-с4,7*х4,7)
t′3,4=t5,6(1-с5,6*х5,5)
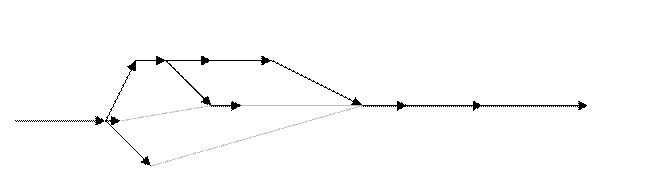
до оптимизации
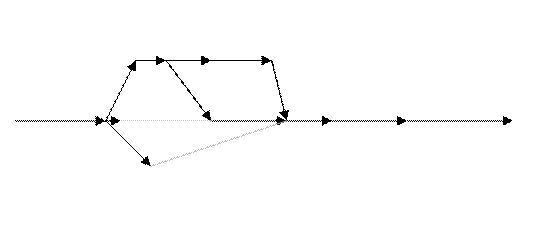
после первого этапа оптимизации

после второго этапа оптимизации
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0 2 4 6 8 10 12 14 16
18 20 22 24 26 28 30 32 34 36 38 40 дни
0 2 4 6 8 10 12 14 16
18 20 22 24 26 28 30 32 34 36 38 40 дни

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.