задачей линейного программирования в симметричной (стандартной)форме записи
2.задачей динамического программирования
3.задачей линейного программирования в канонической (основной) форме записи
4.задачей нелинейного программирования
5.общей задачей линейного программирования
17.
Задача
F = c![]() + c
+ c![]()
![]()
![]()
![]()
![]() .
.
является задачей:
1.задачей линейного программирования в симметричной (стандартной) форме записи
2.задачей динамического программирования
3.задачей линейного программирования в канонической (основной) форме записи
4.задачей нелинейного программирования
5.общей задачей линейного программирования
18.
Задача
F = c![]() + c
+ c![]()
![]()
![]()
![]()
![]() .
.
является задачей:
1.задачей линейного программирования в симметричной (стандартной) форме записи
2.задачей динамического программирования
3.задачей линейного программирования в канонической (основной) форме записи
4.задачей нелинейного программирования
5.общей задачей линейного программирования
19.
Задача
F = c![]() + c
+ c![]()
![]()
![]()
![]()
![]() .
.
является задачей:
1.задачей линейного программирования в симметричной (стандартной) форме записи
2.задачей динамического программирования
3.задачей линейного программирования в канонической (основной) форме записи
4.задачей нелинейного программирования
5.общей задачей линейного программирования
20.
Пусть функция f(x) 8 раз дифференцируется в точке х=а и в этой точке все производные до седьмого порядка включительно равны нулю, а
![]() ≠0 Тогда если
≠0 Тогда если ![]()
![]() 0 то в точке х=а имеем:
0 то в точке х=а имеем:
1.локальный максимум
2.f(x)=0
3.точку перегиба
4.локальный минимум
5.f(x)=∞
21.
При графическом решении задачи нелинейного программирования получена геометрическая интерпретация задачи в виде:
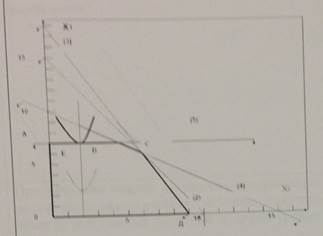
В этом случае задача:
1.имеет область задания, неограниченную снизу
2.имеет единственное решение
3.несовместна
4.имеет бесконечно много решений
5.имеет область задания, неограниченна сверху
22.
При решении задачи
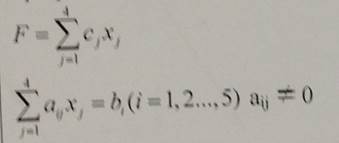
следует использовать:
1.метод производных
2.метод множителей Лагранжа
3.графоаналитический метод
4.однофазный симплекс-метод
5.двухфазный симплекс-метод
23.
Свойства продукции, обусловливающие оптимальное распределение затрат материалов, времени и средств труда при технологической подготовке производства, изготовлении и эксплуатации продукции характеризуют показатели:
1.назначения
2.надежности
3.патентоспособности
4.безопасности
5.технологичности
24.
Точка
![]() представляет ... функции f(x) на множестве
Х, если х*€ Х и
представляет ... функции f(x) на множестве
Х, если х*€ Х и
f(![]() )
)![]() f(x)
f(x)
для всех х € Х.
1.глобальный минимум
2.точку, в которой f(x)=∞
3.точку, в которой f(x)=0
4.глобальный максимум
5.точку перегрева
25.
Точка
![]() представляет ... функции f(x) на множестве
Х, если х*€ Х и
представляет ... функции f(x) на множестве
Х, если х*€ Х и
f(![]() )
)![]() f(x)
f(x)
для всех х € Х.
1.строгий минимум
2.строгий максимум
3.нестрогий минимум
4.нестрогий максимум
5.точку перегрева
26.
При решении задачи линейного программирования графоаналитическим методом получена область допустимых значений и линии уровня.
Задача имеет:
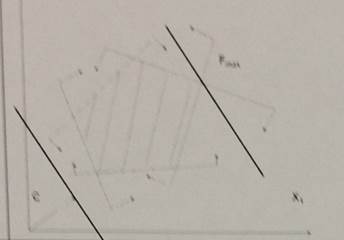
1.единственное решение
2.не имеет решения
3.имеет бесконечно много решений
4.область задания не ограничена сверху
5.область задания не ограничена снизу
27.
При решении задачи линейного программирования графоаналитическим методом получена область допустимых значений и линии уровня.
Задача имеет:
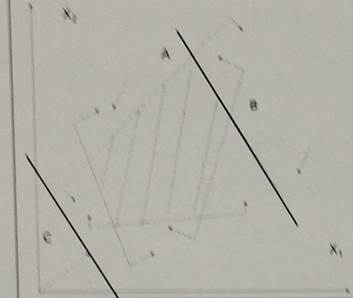
1.единственное решение
2.не имеет решения
3.имеет бесконечно много решений
4.область задания не ограничена сверху
5.область задания не ограничена
28.
При решении задачи линейного программирования графоаналитическим методом получена область допустимых значений и линии уровня.
Задача имеет:

1.единственное решение
2.не имеет решения
3.имеет бесконечно много решений
4.область задания не ограничена сверху
5.область задания не ограничена
29.
Задача
F = ![]() +
+ ![]()
![]()
![]()
![]()
![]() .
.
является задачей:
1.задачей линейного программирования в симметричной (стандартной) форме записи
2.задачей нелинейного программирования
3.задачей линейного программирования в канонической (основной) форме записи
4.задачей динамического программирования
5.общей задачей линейного программирования
30.
При
графическом решении задачи нелинейного программирования с целевой функцией F = ![]() +
+ ![]()
получено следующее множество допустимых решений в виде:
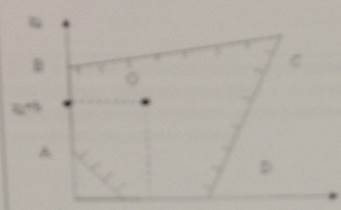
Минимум целевой функции достигается в точке:
1.О
2.С
3.D
4.А
5.В
31.
При
графическом решении задачи нелинейного программирования с целевой функцией F = ![]() -
- ![]()
получено следующее множество допустимых решений в виде:
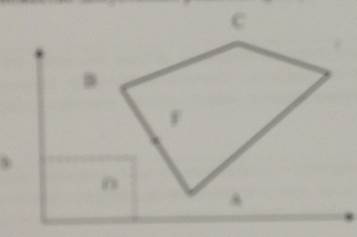
Минимум целевой функции достигается в точке:
1.D
2.C
3.B
4.O
5.A
32.
Особенность продукции, обусловленная при ее ..... или потребности безопасности человека характеризует показатель:
1.назначения
2.безопасности
3.технологичности
4.надежности
5. патентоспособности
33.
Если при решении задачи нелинейного программирования на минимум среди элементов нулевой строки симплекс-таблицы есть положительное, то:
1.текущее базисное решение оптимально
2. текущее базисное решение не является оптимальным
3.задача не имеет решения
4.задача имеет бесконечно много решений
5.задача является вырожденной
34.
Если при решении задачи линейного программирования на минимум среди элементов нулевой строки симплекс-таблицы есть положительное, то:
1.текущее базисное решение оптимально
2. текущее базисное решение не является оптимальным
3.задача не имеет решения
4.задача имеет бесконечно много решений
5.задача является вырожденной
35.
Если в задаче математического программирования целевая функция линейна, а область допустимых решений ограничена и ограничения нелинейные, то данная задача:
1.является задачей линейного программирования
2.является задачей нелинейного программирования
3.является задачей динамического программирования
4.может быть решена однофазным симплекс-методом
5.может быть решена двухфазным симплекс-методом
36.
Задача динамического программирования - это задача:
1.линейного программирования
2.дискретная задача математического программирования
3.которая может быть решена однофазным симплекс-методом
4.которая может быть решена двухфазным симплекс-методом
5.квадратичного программирования
37.
При решении задачи нелинейного программирования графоаналитическим методом на максимум находим линию уровня, которая имеет:
1.d=max
2.d=min
3.d=0
4.d=∞
5.d=1
38.
При решении задачи нелинейного программирования графоаналитическим методом на минимум находим линию уровня, которая имеет:
1.d=max
2.d=min
3.d=0
4.d=∞
5.d=1
39.
Показатель патентной чистоты относится к группе показателей:
1.назначения
2.надежности
3.технологические
4.патентоспособности
5.стандартизации и унификации
40.
Ремонтнопригодность относится к группе показателей:
1.технологические
2.назначения
3.патентно-правовые
4.надежности
5.эргономические
41.
Если при решении задачи нелинейного программирования область допустимых решений ограничена, а линии уровня являются окружностями, центр которых находится в области допустимых решений, то минимум целевой функции находится:
1.в центре окружности
2.в максимально удаленной точке области допустимых решений
3.вне области допустимых решений
4.в бесконечности
5.в минус бесконечности
42.
Если при решении задачи нелинейного программирования область допустимых решений ограничена, а линии уровня являются окружностями, центр которых находится в области допустимых решений, то максимум целевой функции находится:
1.в центре окружности
2.в максимально удаленной точке области допустимых решений
3.вне области допустимых решений
4.в бесконечности
5.в минус бесконечности
43.
Если при решении задачи нелинейного программирования область
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.