Анализ и оптимизация сетевой модели – планирование поставки товаров оптовым покупателям

Министерство образования Российской Федерации

Государственное образовательное учреждение высшего

профессионального образования Комсомольский-на-Амуре

Государственный Технический Университет

Ванинский филиал

КОНТРОЛЬНАЯ РАБОТА

ПО ДИСЦИПЛИНЕ:

Теория систем и системный анализ

Выполнил:

Сергей Владимирович Красюк

682880, г. Советская Гавань,

ул. Бошняка, 4 – 12

Группа: 2ПИа-1В

Ванино 2005

Цель работы:

Найти оптимальное время выполнения поставок оптовым покупателям. Провести анализ и оптимизацию сетевой модели – планирование поставки товаров оптовым покупателям.

Необходимым свойством системы планирования и управления работами является способность оценить текущее состояние, учесть возможное состояние в будущем, предсказать дальнейший ход работ и таким образом предупредить от возможных ошибок, заранее оперативно воздействовать на ход комплекса работ в сжатые сроки и с наименьшими затратами

Особенность СПУ заключается в том, что деятельность всех коллективов исполнителей рассматривается в целом как единый комплекс взаимосвязанных и взаимозависимых операций, направленных на достижение общей конечной цели. Здесь используется информационно-динамическая модель особого вида, так называемая сетевая модель логико-математического описания, позволяющая алгоритмизировать расчеты параметров этого процесса: продолжительности, трудоемкости, стоимости и т.д. Системы рассчитаны на использование компьютерных систем обработки исходных и оперативных данных для расчета контролируемых показателей и получения необходимых аналитических и отчетных сводок.

Методы и модели СПУ могут с успехом применяться в коммерческой деятельности при выполнении различных комплексов работ, а также многих комплексов финансово-коммерческих операций.

Планирование поставки товаров оптовым покупателям.

Рассмотрим оптимизацию по длительности выполнения проекта – планирования поставки товаров оптовым покупателям. Сведём исходные данные к проекту в таблицу 1.1.

Таблица 1.1

Содержание работы	Работа			Длитель-ность работы, дни
	Обозна-чение, Аi	Предшест-вующие работы	Коэффи-циент пересчёта,  С
Отбор товара	А1	-	0,1	6
Подготовка к отправке	А2	А1	0,2	5
Определение объёма отгрузки	А3	А1	0,3	4
Проверка цен	А4	А1	0,4	2
Оформление счёта	А5	А4	0,6	4
Выписка накладной	А6	А5	0,5	3
Заказ автомашины	А7	А3, А6	0,7	2
Отправка счёта покупателю	А8	А5	1,1	3
Проверка товаров по счёту	А9	А8	0,9	2
Оплата счёта	А10	А9	0,3	6
Погрузка товара и проверка количества	А11	А2, А7, А10	1,2	1
Перевозка товара	А12	А11	0,5	6
Выгрузка и сверка с документами	А13	А12	0,6	5

Построим сетевой график по данным, приведённым в таблице 1.1.

 

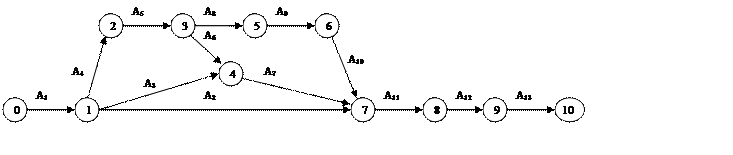Рис. 1. График по данным таблицы 1.1.

Определим пути, присутствующие в сетевом графике. Таких путей можно выделить четыре. В первый путь (L₁) входят работы А₁, А₄, А₅, А₈, А₉, А₁₀, А₁₁, А₁₂, А₁₃. Во второй путь (L₂) входят работы А₁, А₄, А₅, А₆, А₇, А₁₁, А₁₂, А₁₃. В третий путь (L₃) входят работы А₁, А₃, А₇, А₁₁, А₁₂, А₁₃. В четвёртый путь (L₄) входят работы А₁, А₂, А₁₁, А₁₂, А₁₃. Рассчитаем длительности всех четырёх путей:

 дней;

 дней;

 дней;

 дня.

Результаты расчёта показывают, что критическим является первый путь. Решение задачи оптимизации состоит в последовательном переносе средств с некритических работ на критические, переходе от одного пути к другому до тех пор, пока все работы не будут критическими и не будут иметь резервов, а длительности всех путей станут равными. Для определения резервов рассчитаем параметры сетевого графика. Результаты расчётов сведём в таблице 1.2.

Таблица 1.2.

Работа	Количество предшест-вующих работ	Продолжи-тельность работ	Сроки выполнения работ				Резервы времени
			Ранние		Поздние		работ		Собы-тий
			На-чало	Окон-чание	На-чало	Окон-чание	Пол-ный	Сво-бод-ный
А1 (0-1)	0	6	0	6	0	6	0	0	0
А2 (1-7)	1	5	6	11	18	23	12	12	0
А3 (1-4)	1	4	6	10	17	21	11	5	6
А4 (1-2)	1	2	6	8	6	8	0	0	0
А5 (2-3)	1	4	8	12	8	12	0	0	0
А6 (3-4)	1	3	12	15	18	21	6	0	6
А7 (4-7)	2	2	15	17	21	23	6	6	0
А8 (3-5)	1	3	12	15	12	15	0	0	0
А9 (5-6)	1	2	15	17	15	17	0	0	0
А10 (6-7)	1	6	17	23	17	23	0	0	0
А11 (7-8)	3	1	23	24	23	24	0	0	0
А12 (8-9)	1	6	24	30	24	30	0	0	0
А13 (9-10)	1	5	30	35	30	35	0	0	0

Начнём оптимизировать сетевой график.Определим путь, ближайший по длительности к критическому. Учитывая расчёты путей, сделанные выше, приходим к выводу, что таким путём является второй путь. Длительность этого пути равна 29 дням, и соответственно свободный резерв времени составляет 6 дней. Будем переносить средства с работы А₇ (4-7), находящейся на подкритическом пути L₂, на работу А₁₀ (6-7), находящуюся на критическом пути. Условие допустимости решения по величине переносимых средств выглядит так:

.

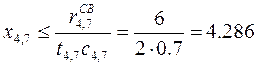Запишем систему уравнений, с помощью которой можно определить величину переносимых средств:

.

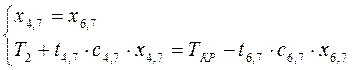Подставим численные значения и решим эту систему:

.

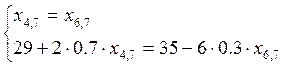Полученное решение имеет следующий вид:

.

Проверяем на допустимость переносимых средств:

 - решение допустимо.

Найдём новые длительности работ А₇ (4-7) и А₁₀ (6-7) по формулам:

,

.

Подставив значения, получим:

,

.

Определим новые длительности путей, суммируя длительности работ, входящих в соответствующие пути:

.

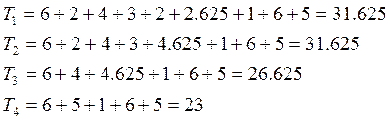Перейдём ко второму этапу оптимизации. Определим путь, ближайший по длительности к критическому. Учитывая расчёты путей, сделанные выше, приходим к выводу, что таким путём является третий путь. Длительность этого пути равна 26,625 дней, и соответственно свободный резерв времени составляет 5 дней. Будем переносить средства с работы А₃ (1-4), находящейся на подкритическом пути L₃, на работы